题目内容
10. 如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.
如图,点E为正方形ABCD的边CD的中点,点F在AD上,CF交AE于点G,且∠CGE=45°,AE=$\sqrt{5}$,则CF的长为$\frac{2}{3}$$\sqrt{10}$.
分析 连接AC,作FM⊥AC于M,首先证明△ADE∽△CMF得到CM=2FM,设AM=FM=a,列出方程求出a,即可解决问题.
解答 解: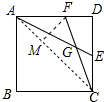 连接AC,作FM⊥AC于M.
连接AC,作FM⊥AC于M.
∵四边形ABCD是正方形,
∴AD=CD,∠D=∠BAD=90°,∠DAC=45°,
∵∠AMF=90°,
∴∠MAF=∠MFA=45°,
∴AM=FM.设AM=FM=a,AD=2b.则DE=EC=b,
在RT△ADE中,∵AD2+DE2=AE2,
∴5=5b2,
∵b>0,
∴b=1,AD=2,DE=1,
∵∠EGC=∠GAC+∠GCA=45°,∠GAC+∠DAE=45°,
∴∠DAE=∠FCM,
∵∠FMC=∠ADE=90°,
∴△ADE∽△CMF,
∴$\frac{AD}{CM}$=$\frac{DE}{FM}$,
∴$\frac{CM}{FM}$=$\frac{AD}{DE}$=2,
∴CM=2FM,
∴2$\sqrt{2}$-a=2a,
∴a=$\frac{2}{3}$$\sqrt{2}$,
∴FM=$\frac{2}{3}$$\sqrt{2}$,CM=$\frac{4}{3}$$\sqrt{2}$,
∴CF=$\sqrt{C{M}^{2}+F{M}^{2}}$=$\sqrt{(\frac{2\sqrt{2}}{3})^{2}+(\frac{4\sqrt{2}}{3})^{2}}$=$\frac{2}{3}$$\sqrt{10}$.
故答案为$\frac{2}{3}$$\sqrt{10}$.
点评 本题考查正方形的性质、相似三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.

练习册系列答案
相关题目
 如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).
如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).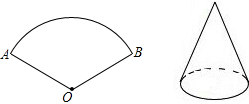 如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm.
如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm. 已知关于x的一次函数y=kx+4的图象经过点(1,2).
已知关于x的一次函数y=kx+4的图象经过点(1,2).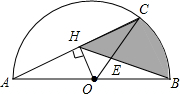 如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.
如图,AB为半圆的直径,弧AC为弧CB的两倍,OH⊥AC于点H,BH与OC交于E,己知AC=2$\sqrt{3}$.