题目内容
20.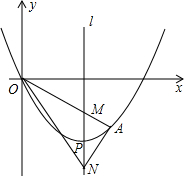 如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
如图,抛物线y=$\frac{1}{4}$(x-4)2-4的顶点为P,M,N均在对称轴上,且PM=PN,延长OM交抛物线于点A,求证:∠ANM=∠ONM.
分析 过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证.
解答 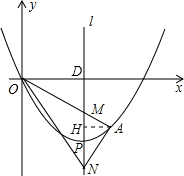 证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:
证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:
设A(m,$\frac{1}{4}$m2-2m),又O(0,0),
∴直线AO的解析式为y=$\frac{\frac{1}{4}{m}^{2}-2m}{m}$x=($\frac{1}{4}$m-2)x,
则M(4,m-8),N(4,-m),H(4,$\frac{1}{4}$m2-2m),
∴OD=4,ND=m,HA=m-4,NH=ND-HD=$\frac{1}{4}$m2-m,
在Rt△OND中,tan∠ONM=$\frac{OD}{DN}$=$\frac{4}{m}$,
在Rt△ANH中,tan∠ANM=$\frac{HA}{HN}$=$\frac{m-4}{\frac{1}{4}{m}^{2}-m}$=$\frac{4(m-4)}{m(m-4)}$=$\frac{4}{m}$,
∴tan∠ONM=tan∠ANM,
∴∠ANM=∠ONM.
点评 本题考查了两点坐标确定一次函数解析式,锐角三角函数定义,等腰直角三角形的判定与性质,勾股定理,以及相似三角形的判定与性质,是一道综合性的题目,难度中等.

练习册系列答案
相关题目

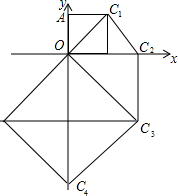 如图,点A是y轴上的一点,以线段OA为边作第1个正方形,得到对角线OC1,再以OC1为边作第2个正方形,得到对角线OC2,再以OC2为边作第3个正方形,得到对角线OC3,再以OC3为边作第4个正方形,得到对角线OC4,…,以此类推,得到正方形对角线OC2017,若OA的长度为1,则点C2017的坐标是(21008,21008).
如图,点A是y轴上的一点,以线段OA为边作第1个正方形,得到对角线OC1,再以OC1为边作第2个正方形,得到对角线OC2,再以OC2为边作第3个正方形,得到对角线OC3,再以OC3为边作第4个正方形,得到对角线OC4,…,以此类推,得到正方形对角线OC2017,若OA的长度为1,则点C2017的坐标是(21008,21008).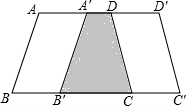 如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?
如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=6cm.梯形ABCD的高为5cm、试问将梯形ABCD沿着AD方向平移多少厘米才能使平移后的梯形与原来的梯形ABCD重叠部分的面积为10cm2?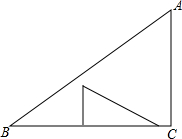 在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和.
在△ABC中,∠C=90°,AC=3,BC=4,两直角边分别为1,2的三角形纸片按如图所示放置,若该纸片在△ABC内任意平移,求△ABC内不能被平移到的部分的面积和.