��Ŀ����
3���Ķ����в��ϣ������������⣺����֪������2x+3y=12���������⣬����ʵ������������ֻ��������������⣮
������2x+3y=12���ã�y=$\frac{12-2x}{3}$=4-$\frac{2}{3}$x��x��yΪ����������Ҫʹy=4-$\frac{2}{3}$xΪ����������$\frac{2}{3}$xΪ����������֪��xΪ3�ı������Ӷ�x=3������y=4-$\frac{2}{3}$x=2������2x+3y=12����������Ϊ$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$��
���⣺
��1������ֱ��д������3x+2y=8����������$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$��
��2����$\frac{6}{x-3}$Ϊ��Ȼ����������������������x��ֵ��B
A��3�� B��4�� C��5�� D��6��
��3������x��y�Ķ�Ԫһ�η�����$\left\{\begin{array}{l}{x+2y=9}\\{2x+ky=10}\end{array}\right.$�Ľ�����������������k��ֵ��
���� ��1�����ݶ�Ԫһ�η��̵Ľ�ö���������ɣ�
��2����������ó�x-3=6��3��2��1��������ɣ�
��3�������y��ֵ���������k��ֵ��
��� �⣺��1������3x+2y=8����������Ϊ$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$��
�ʴ�Ϊ$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$��
��2����������9��6��5��4����4����
��ѡB��
��3��$\left\{\begin{array}{l}{x+2y=9��}\\{2x+ky=10��}\end{array}\right.$
�١�2-�ڵã���4-k��y=8��
��ã�y=$\frac{8}{4-k}$��
��x��y����������k��������
4-k=1��2��4��8��
��k=3��2��0��-4��
��k=3ʱ��x��������������k=2��0��-4��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬��Ԫһ�η��̵Ľ��Ӧ�ã����������֪ʶ�����������ǽ����Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
3������ѧ��ͨ�������ĵ�����ƣ�ij�ֶ���20��ĸ���Ϊ0.8���25��ĸ���Ϊ0.6��������20������ֶ���25��ĸ����ǣ�������
| A�� | 0.8 | B�� | 0.75 | C�� | 0.6 | D�� | 0.48 |
14������m+2��x${\;}^{{m}^{2}-3}$-2m=1���ǹ���x��һԪһ�η��̣���m=��������
| A�� | ��2 | B�� | 2 | C�� | -2 | D�� | 1 |
18������-3+|-5|�Ľ���ǣ�������
| A�� | -2 | B�� | 2 | C�� | -8 | D�� | 8 |
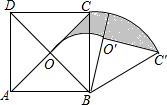 ��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OBC�Ƶ�B˳ʱ����ת60��õ���0��BC�䣬��AB=2����ͼ����Ӱ���ֵ������ $\frac{��}{3}$��
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OBC�Ƶ�B˳ʱ����ת60��õ���0��BC�䣬��AB=2����ͼ����Ӱ���ֵ������ $\frac{��}{3}$��