题目内容
7. 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:(1)猜想△CMN的形状,并证明你的结论;
(2)请你证明CN是⊙O的切线;
(3)若等边△ABC的边长是2,求AD•AM的值.
分析 (1)根据全等三角形的判定定理得到△BCN≌△ACM,由全等三角形的性质得到CN=CM,∠BCN=∠ACM,求得∠MCN=∠ACB=60°,即可得到结论;
(2)根据全等三角形的性质得到∠ACO=∠BCO=$\frac{1}{2}∠$ACB=30°,根据角的和差得到∠OCN=90°,根据切线的判定定理得到结论;
(3)根据相似三角形的判定和性质即可得到结论.
解答  解:(1)△CMN是等边三角形,
解:(1)△CMN是等边三角形,
理由:在△BCN与△ACM中,$\left\{\begin{array}{l}{BC=AC}\\{∠CBN=∠CAM}\\{BN=AM}\end{array}\right.$,
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠BCN-∠ACN=∠ACM-∠ACN,
即∠MCN=∠ACB=60°,
∴△CMN是等边三角形;
(2)连接OA.OB.OC,
在△BOC与△AOC中,$\left\{\begin{array}{l}{OA=OB}\\{AC=BC}\\{OC=OC}\end{array}\right.$,
∴△BOC≌△AOC,
∴∠ACO=∠BCO=$\frac{1}{2}∠$ACB=30°,
∵∠ACB=∠MCN=60°,
∴∠ACN=60°,
∴∠OCN=90°,
∴OC⊥CN,
∴CN是⊙O的切线;
(3)∵∠ADB=∠ACB=60°,
∴∠ADB=∠ABC,
∵∠BAD=∠MAB,
∴△ABD∽△AMB,
∴$\frac{AB}{AM}=\frac{AD}{AB}$,
∴AD•AM=AB2=22=4.
点评 本题考查了切线的判定,全等三角形的判定和性质,相似三角形的判定和性质,等边三角形的判定和性质,熟练正确相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
17. 如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
(1)求该抛物线的解析式
(2)连结CD,BD,求四边形OCDB的面积.
 如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)
如图,在平面直角坐标系中,抛物线的顶点为D(1,4),与y轴相交于点C(0,3),与x轴相交于A、B两点(点A在点B的左侧)(1)求该抛物线的解析式
(2)连结CD,BD,求四边形OCDB的面积.
15.已知⊙O的半径为5cm,圆内两平行弦AB、CD的长分别为6cm、8cm,则弦AB、CD间的距离为( )
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
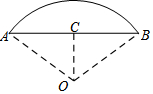 如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.
如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.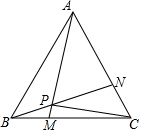 如图,等边△ABC的边长是6,动点M、N分别同时从B、C出发,沿边BC、CA以1个单位/秒的速度运动(动点M、N分别到达C、A时停止运动),AM、BN交于点P,运动时间是t秒.
如图,等边△ABC的边长是6,动点M、N分别同时从B、C出发,沿边BC、CA以1个单位/秒的速度运动(动点M、N分别到达C、A时停止运动),AM、BN交于点P,运动时间是t秒.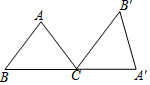 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.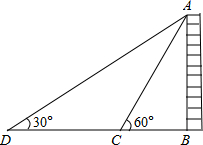 如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).
如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).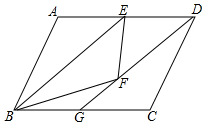 如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.
如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.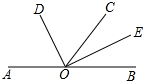 如图,点A、O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,已知∠AOC=150°,求∠DOE的度数.
如图,点A、O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,已知∠AOC=150°,求∠DOE的度数.