题目内容
2.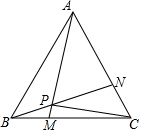 如图,等边△ABC的边长是6,动点M、N分别同时从B、C出发,沿边BC、CA以1个单位/秒的速度运动(动点M、N分别到达C、A时停止运动),AM、BN交于点P,运动时间是t秒.
如图,等边△ABC的边长是6,动点M、N分别同时从B、C出发,沿边BC、CA以1个单位/秒的速度运动(动点M、N分别到达C、A时停止运动),AM、BN交于点P,运动时间是t秒.(1)①求证:AM=BN;②求∠BPM的度数;
(2)连接PC,当PC⊥AM时,求t的值;
(3)当M从点B运动至点C时,直接写出点P运动的路径长.
分析 (1)①轨迹等边三角形的性质、全等三角形的判定定理证明△ABM≌△BCN,得到AM=BN;
②根据全等三角形的性质、三角形的外角的性质计算即可;
(2)根据圆内接四边形的判定和性质得到∠MNC=∠MPC=90°,根据∠NCM=60°列出方程,解方程即可;
(3)根据题意确定点P运动的路径长,根据弧长公式计算即可.
解答 解:(1)①由题意得,BM=CN,∠ABC=∠ACB=60°,
在△ABM和△BCN中,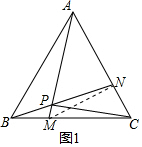
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠BCN}\\{BM=CN}\end{array}\right.$,
∴△ABM≌△BCN,
∴AM=BN;
②∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∴∠BPM=∠ABP+∠BAM=∠ABP+∠CBN=60°;
(2)连接MN,
∵∠APN=∠ACM=60°,
∴P、M、C、N四点共圆,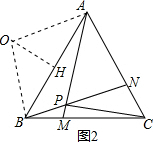
∴∠MNC=∠MPC=90°,
∵∠NCM=60°,
∴MC=2CN,即6-t=2t,
解得,t=2,
答:当PC⊥AM时,t=2;
(3)∵∠BPM=60°,
∴∠APB=120°,
∴点P运动的路径长是以AB为弦、圆周角∠APB=120°的弓形的弧长,
如图2,∵∠APB=120°,
∴∠AOB=120°,
∴OB=$\frac{BH}{sin∠BOH}$=2$\sqrt{3}$,
点P运动的路径长为:$\frac{120π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}}{3}π$.
点评 本题考查的是全等三角形的判定和性质、直角三角形的性质、点的轨迹的确定,掌握全等三角形的判定定理和性质定理、直角三角形的性质是解题的关键.

练习册系列答案
相关题目
12.下列各数中最小的是( )
| A. | -2016 | B. | $\frac{1}{2016}$ | C. | -$\frac{1}{2016}$ | D. | 2016 |
10.下列方程中一定是关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | 3(x+1)2=2(x+1) | D. | x2-x(x+7)=0 |
11.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
 使用五点法画出二次函数y=x2-2x-3的图象.
使用五点法画出二次函数y=x2-2x-3的图象. 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
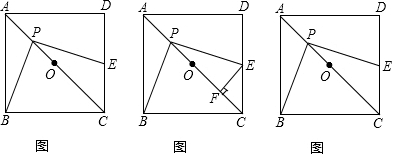
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题: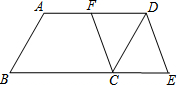 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF.
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF.