题目内容
19.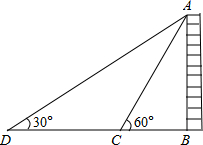 如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).
如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30°,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60°,则此楼房的高度为5$\sqrt{3}$米(结果保留根号).
分析 首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及CD=BD-BC=10构造方程关系式,进而可解,即可求出答案.
解答 解:∵在直角三角形ADB中,∠D=30°,
∴$\frac{AB}{BD}$=tan30°,
∴BD=$\frac{AB}{tan30°}$=$\sqrt{3}$AB,
∵在直角三角形ABC中,∠ACB=60°,
∴BC=$\frac{AB}{tan60°}$=$\frac{\sqrt{3}}{3}$AB,
∵CD=10,
∴CD=BD-BC=$\sqrt{3}$AB-$\frac{\sqrt{3}}{3}$AB=10,
解得:AB=5$\sqrt{3}$.
故答案为:5$\sqrt{3}$.
点评 本题考查解直角三角形的应用-仰角俯角问题,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列方程中一定是关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | 3(x+1)2=2(x+1) | D. | x2-x(x+7)=0 |
4.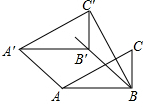 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )| A. | 6 | B. | 5 | C. | 4$\sqrt{2}$+1 | D. | $\sqrt{41}$ |
11.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
9.下列几何体中,从正面看所得到的图形是圆的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知点A,B.
如图,已知点A,B. 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题: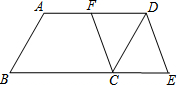 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF.
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连接DE,CF.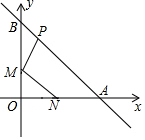 如图所示,已知点N(1,0),直线y=-x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.
如图所示,已知点N(1,0),直线y=-x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.