题目内容
16.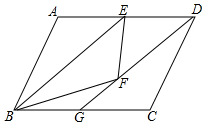 如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.
如图,?ABCD中,E为AD边的中点,把△ABE沿BE翻折,得到△FBE,连接DF并延长交BC于G.(1)求证:四边形BEDG为平行四边形.
(2)若BE=AD=10,且?ABCD的面积等于60,求FG的长.
分析 (1)根据折的性质得到AE=EF,∠AEB=∠FEB,由平角的定义得到∠AEB=$\frac{1}{2}$(180°-∠DEF),由三角形的内角和得到∠EDF=$\frac{1}{2}$(180°-∠DEF),根据平行四边形的判定定理即可得到结论;
(2)由平行四边形的性质得到DE=BG,DG=BE=10,S△ABE=$\frac{1}{4}$S平行四边形ABCD=15,连接AF交BE于H,于是得到AH⊥BE,AH=HF,根据勾股定理即可得到结论.
解答 (1)证明:∵把△ABE沿BE翻折,得到△FBE,
∴AE=EF,∠AEB=∠FEB,
∴∠AEB=$\frac{1}{2}$(180°-∠DEF),
∵E为AD边的中点,
∴AE=DE,
∴DE=EF,
∴∠EDF=∠EFD,
∴∠EDF=$\frac{1}{2}$(180°-∠DEF),
∴∠AEB=∠EDF,
∴BE∥DG,
∵四边形ABCD是平行四边形,
∴DE∥BG,
∴四边形BEDG为平行四边形;
(2)解:如图,∵四边形BEDG为平行四边形,
∴DE=BG,DG=BE=10,
∵四边形ABCD是平行四边形,AE=DE,?ABCD的面积等于60,
∴S△ABE=$\frac{1}{4}$S平行四边形ABCD=15,
连接AF交BE于H,则AH⊥BE,AH=HF,
∵BE=10,
∴AH=3,
∴AF=6,
∵BE∥DG,
∴AF⊥DG,
∴DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=8,
∴FG=DG-FD=2.
点评 本题考查了翻折变换(折叠问题),平行四边形的判定和性质,勾股定理,熟练正确折叠的性质是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
4.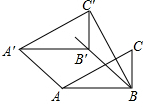 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′,连结AA′,BC′.若BB′=4$\sqrt{2}$,则BC′的长为( )| A. | 6 | B. | 5 | C. | 4$\sqrt{2}$+1 | D. | $\sqrt{41}$ |
11.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
③当x=2时,y=5;④3是方程ax2+(b-1)x+c=0的一个根;
其中正确的有①③④.(填正确结论的序号)
5.下列等式变形错误的是( )
| A. | 由x=y,得x+5=y+5 | B. | 由x=y,得$\frac{x}{-2}$=$\frac{y}{-2}$ | ||
| C. | 由-3x=-3y,得x=-y | D. | 由x-1=y-1,得x=y |
 如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).
如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504). 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题: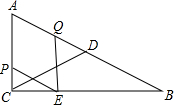 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中线,动点P从点C出发,沿CA以每秒1个单位长度的速度向终点A运动,同时,动点Q从点A出发,沿AB以每秒2个单位长度向终点B运动,过点P作PE∥AB,连结EQ,设点P运动的时间为t(s)(t>0)
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中线,动点P从点C出发,沿CA以每秒1个单位长度的速度向终点A运动,同时,动点Q从点A出发,沿AB以每秒2个单位长度向终点B运动,过点P作PE∥AB,连结EQ,设点P运动的时间为t(s)(t>0)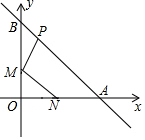 如图所示,已知点N(1,0),直线y=-x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.
如图所示,已知点N(1,0),直线y=-x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是$\frac{3\sqrt{2}}{2}$.