题目内容
3.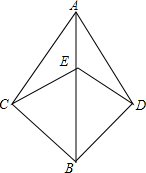 如图,AC=AD,BC=BD,点E在AB上.
如图,AC=AD,BC=BD,点E在AB上.(1)你能找出3对全等三角形;
(2)请你同时运用“SSS”和“SAS”证明其中找出的一对全等三角形.
分析 (1)可以找到△ACE≌△ADE,△BCE≌△BDE,△ABC≌△ABD;
(2)由于AC=AD,BC=BD,加上公共边AB,则利用“SSS”可证明△ABC≌△ABD;根据线段垂直平分线的判定方法可得到AB平分∠CAD,则利用等腰三角形的性质得∠CAB=∠DAB,于是可利用“SAS”可证明△ABC≌△ABD.
解答 解:(1)△ACE≌△ADE,△BCE≌△BDE,△ABC≌△ABD;
故答案为3;
(2)证明△ABC≌△ABD的过程如下:
方法一:在△ABC和△ABD中
$\left\{\begin{array}{l}{AC=AD}\\{BC=BD}\\{AB=AB}\end{array}\right.$,
∴△ABC≌△ABD(SSS);
方法二:连结CD,如图,
∵AC=AD,BC=BD,
∴AB垂直平分CD,
∴AB平分∠CAD,
∴∠CAB=∠DAB,
在△ABC和△ABD中
$\left\{\begin{array}{l}{AC=AD}\\{∠CAB=∠DAB}\\{AB=AB}\end{array}\right.$,
∴△ABC≌△ABD(SAS).
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列图形中,旋转对称图形有( )个.


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.已知点C在线段AB的延长线上,5CB=2AC,则$\frac{AC}{AB}$的值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
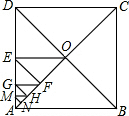 如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )
如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )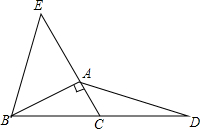 已知:如图,Rt△ABC中,∠BAC=90°,延长BC到点D,使CD=BC,延长CA到点E,使AE=2CA;连接AD,BE.求证:AD=BE.
已知:如图,Rt△ABC中,∠BAC=90°,延长BC到点D,使CD=BC,延长CA到点E,使AE=2CA;连接AD,BE.求证:AD=BE.