题目内容
3.若3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,则m的值为( )| A. | 56 | B. | 34 | C. | 28 | D. | 14 |
分析 先求出$\sqrt{m}$的值,进而可得出结论.
解答 解:∵3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,
∴$\sqrt{m}$=5$\sqrt{7}$-3$\sqrt{7}$=2$\sqrt{7}$=$\sqrt{28}$,
∴m=28.
故选C.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
17.下列等式一定成立的是( )
| A. | a3•a3=a9 | B. | (a3)2=a5 | C. | (2ab2)3=6a3b6 | D. | (-a)7÷(-a)2=-a5 |
14.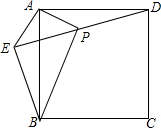 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:①△APD≌△AEB;
②点B到直线AE的距离为$\sqrt{3}$;
③EB⊥ED;
④S△APD+S△APB=1+$\sqrt{2}$
⑤S正方形ABCD=5+2$\sqrt{2}$.
其中正确的序号是( )
| A. | ①②③ | B. | ①③⑤ | C. | ②③④ | D. | ①②④ |
8.若427+41000+4n为完全平方数,则正整数n满足( )
| A. | n≥1972 | B. | n≤1972 | C. | n≥1973 | D. | n≤1970 |
12.下列说法:
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.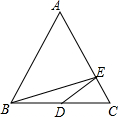 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{3}+1$ |
 如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.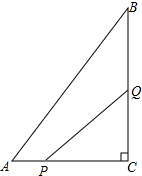 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?