题目内容
11. 如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,菱形ABCD中,对角线AC=$2\sqrt{3}$,BD=2,以A为圆心,AB为半径画圆弧BD,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
分析 根据菱形的性质得到AC⊥BD,由已知条件得到tan∠DAC=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,AD=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,求得∠DAC=30°,得到∠DAB=60°,于是得到结论.
解答 解:在菱形ABCD中,
∵AC⊥BD,
∵AC=$2\sqrt{3}$,BD=2,
∴tan∠DAC=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,AD=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,
∴∠DAC=30°,
∴∠DAB=60°,
∴阴影部分的面积=S菱形ABCD-S扇形ABD=$\frac{1}{2}$×$2\sqrt{3}$×2-$\frac{60π•{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π,
故答案为:2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了扇形的面积 的计算,菱形的性质,勾股定理,三角函数,正确的识别图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若方程组$\left\{\begin{array}{l}{1998x+2006y=2007}\\{(|a|-2)z+5x=5}\end{array}\right.$是二元一次方程组,则a等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
6.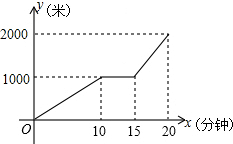 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )| A. | 家到学校的距离是2000米 | |
| B. | 修车耽误的时间是5分钟 | |
| C. | 修车后自行车的速度是每分钟200米 | |
| D. | 修车前比修车后速度快 |
3.若3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,则m的值为( )
| A. | 56 | B. | 34 | C. | 28 | D. | 14 |
1.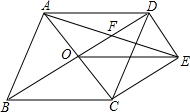 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
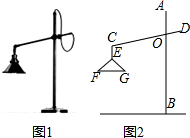 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm. 如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.
如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.