题目内容
8.若427+41000+4n为完全平方数,则正整数n满足( )| A. | n≥1972 | B. | n≤1972 | C. | n≥1973 | D. | n≤1970 |
分析 通过提公因式,把原式整理成完全平方式的形式,从而推出n的值,进而通过反正的方式进行排除选项得解.
解答 解:因为427+41000+4n=254(1+2•21945+22n-54),
所以当2n-54=2×1945,即n=1972时,上式为完全平方数.
当n>1972时,有(2n-27)2<1+2•21945+22n-54<1+2•2n-27+22(n-27)=(2n-27+1)2,
所以上式不可能为完全平方数.
故选B.
点评 此题主要考查了完全平方数,正确利用完全平方数的性质求出n的取值范围是解题关键.

练习册系列答案
相关题目
3.若3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,则m的值为( )
| A. | 56 | B. | 34 | C. | 28 | D. | 14 |
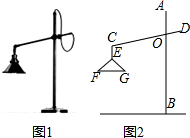 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.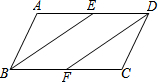 如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.
如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.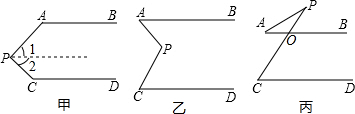 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.