题目内容
15.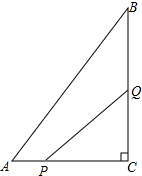 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
分析 设经过x秒钟,△PQC的面积等于8cm2,根据点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止,表示出CP和CQ的长可列方程求解.
解答 解:设P、Q同时出发t秒时,△PBQ的面积等于8cm2,由题意得
$\frac{1}{2}$(6-t)2t=8
解得,t1=2,t2=4,
经检验,t1=2,t2=都4是原方程的解,所以,经过2秒或4秒,△PCQ的面积等于8cm2.
点评 此题主要考查了一元二次方程的应用,找到关键描述语“△PCQ的面积等于8cm2”,得出等量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.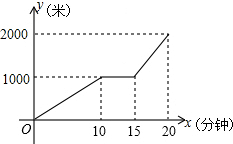 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )| A. | 家到学校的距离是2000米 | |
| B. | 修车耽误的时间是5分钟 | |
| C. | 修车后自行车的速度是每分钟200米 | |
| D. | 修车前比修车后速度快 |
3.若3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,则m的值为( )
| A. | 56 | B. | 34 | C. | 28 | D. | 14 |
7.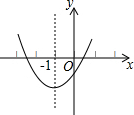 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )| A. | (l)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
5.一元二次方程两个根为1和3,那么这个方程为( )
| A. | x2+4x+3=0 | B. | x2+4x-3=0 | C. | x2-4x+3=0 | D. | x2-4x-3=0 |
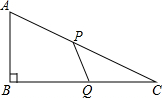 如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒.
如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒. 在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.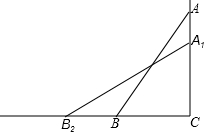 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?