题目内容
12.下列说法:①直径是弦;
②弦是直径;
③过圆上任意一点有无数条弦,且这些弦都相等;
④直径是圆中最长的弦.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 弦是连接圆上两点间的线段,直径是弦,是过圆心的弦,是圆中最长的弦.由弦和直径的定义对这四个命题作出判断.
解答 解:①因为直径的两个端点在圆上,直径是连接圆上这两个端点的线段.所以直径是弦是正确的.
②弦是连接圆上两点的线段,如果过圆心就是直径,不过圆心就不是直径.所以弦是直径不正确.
③过圆内一点是有无数多条弦,但这些弦不一定相等,其中过圆心的弦是最长的.所以③不正确.
④直径是过圆心的弦,当然是圆中最长的弦.所以④正确.
故选B.
点评 本题考查的是对圆的认识,根据弦和直径的概念对每个命题进行分析,然后作出判断和选择.

练习册系列答案
相关题目
3.若3$\sqrt{7}$+$\sqrt{m}$=5$\sqrt{7}$,则m的值为( )
| A. | 56 | B. | 34 | C. | 28 | D. | 14 |
7.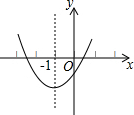 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
 己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )
己知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)abc>0;(2)2a+b=0;(3)a+b+c>0;(4)a-b+c<0,则正确的结论是( )| A. | (l)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
1.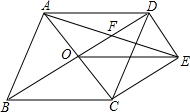 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
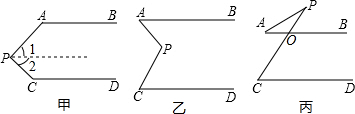 阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.
阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.解:过点P作PE∥AB.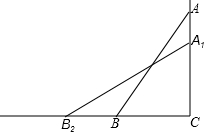 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?
如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?