题目内容
15.一个圆锥的侧面展开图是半径为R的半圆,该圆锥的高是$\frac{\sqrt{3}}{2}$R.分析 根据侧面展开图的弧长等于圆锥的底面周长,即可求得底面周长,进而即可求得底面的半径长,然后表示出圆锥的高即可.
解答 解:圆锥的底面周长是:πR;
设圆锥的底面半径是r,则2πr=πR.
解得:r=$\frac{1}{2}$R.
由勾股定理得到圆锥的高为$\sqrt{{R}^{2}-(\frac{1}{2}R)^{2}}$=$\frac{\sqrt{3}}{2}$R,
故答案为:$\frac{\sqrt{3}}{2}$R.
点评 本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
3.函数y=$\frac{x+3}{\sqrt{x-2}}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≥-3 | C. | x>-3 | D. | x≥2 |
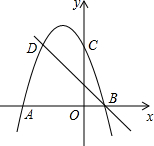
10. 如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
 如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )| A. | y=-x+2 | B. | y=-2x-2 | C. | y=2x+2 | D. | y=-2x+2 |
 如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2,S△ACD为( )
如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2,S△ACD为( ) 画出如图所示几何体的主视图和左视图.
画出如图所示几何体的主视图和左视图.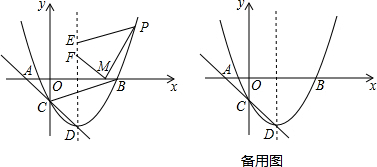
 如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D.
如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D. 如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.
如图,已知二次函数y=x2+bx+c的图象经过点A(-1,0),B(1,-2),该图象与x轴的另一个交点为C,则AC的长为3.