题目内容
5.关于x的不等式组$\left\{\begin{array}{l}{\frac{x+5}{2}>x}\\{\frac{x+1}{2}<x+a}\end{array}\right.$只有3个整数解,则a的取值范围是-0.5<a≤0.分析 首先解每个不等式,然后根据不等式组只有3个整数解,得到整数解,进而得到关于a的不等式,求得a的范围.
解答 解:$\left\{\begin{array}{l}{\frac{x+5}{2}>x…①}\\{\frac{x+1}{2}<x+a…②}\end{array}\right.$,≠
解①得x<5,
解②得x>1-2a.
不等式组有3个整数解,一定是4,3,2.
则1≤1-2a<2
解得:-0.5<a≤0.
故答案是:-0.5<a≤0.
点评 本题考查了不等式组的整数解,先把题目中除未知数外的字母当做常数看待解不等式组,然后再根据题目中对结果的限制的条件得到有关字母的代数式,最后解代数式即可得到答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,n),B(-1,2)是一次函数y=kx+b与反比例函数$y=\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.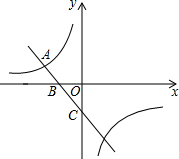 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a).
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x-1的图象的一个交点为A(-2,a). 如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.
如图,已知AD∥BC,∠C=38°,∠ADB:∠BDC=1:3,则∠ADB=35.5°.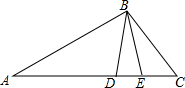 如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE.
如图,在△ABC中,D是AC上一点,AB2=AD•AC,∠CBD的平分线交AC于点E.求证:AB=AE. 反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.
反比例函数y=$\frac{k}{x}$在第一象限的图象如图,请写出一个满足条件的k值,k=3.