题目内容
4.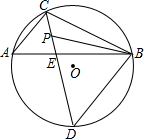 已知,如图,AB为直径,△ABC内接于⊙O,点P是△ABC的内心,延长CP交圆于点D,连接BP.
已知,如图,AB为直径,△ABC内接于⊙O,点P是△ABC的内心,延长CP交圆于点D,连接BP.(1)求证:BD=DP;
(2)已知⊙O的半径是3$\sqrt{2}$,CD=8,求ED的长.
分析 (1)由圆周角定理得出∠ACB=90°,由内心得出∠ACD=∠BCP=45°,∠CBP=∠EBP,∠ABD=∠ACD=45°,由三角形的外角性质得出∠DPB=∠DBP,即可得出结论;
(2)连接AD,由圆周角定理得出∠ABD=45°,证出△ABD是等腰直角三角形,得出BD=$\frac{\sqrt{2}}{2}$AB=6,证明△DBE∽△DCB,得出对应边成比例,即可得出结果.
解答 (1)证明:∵AB为直径,
∴∠ACB=90°,
∵点P是△ABC的内心,
∴∠ACD=∠BCP=45°,∠CBP=∠EBP,
∴∠ABD=∠ACD=45°,
∵∠DPB=∠BCP+∠CBP=45°+∠CBP,∠DBP=∠ABD+∠EBP=45°+∠EBP,
∴∠DPB=∠DBP,
∴BD=DP;
(2)解:连接AD,如图所示: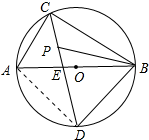
∵AB是直径,∠ABD=45°,
∴AB=6$\sqrt{2}$,△ABD是等腰直角三角形,
∴BD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×6$\sqrt{2}$=6,
∵∠EDB=∠BDC,∠ABD=∠BCD,
∴△DBE∽△DCB,
∴$\frac{BD}{CD}=\frac{DE}{BD}$,
∴DE=$\frac{B{D}^{2}}{CD}$=$\frac{{6}^{2}}{8}$=4.5.
点评 本题考查了三角形的内切圆与内心、圆周角定理、三角形的外角性质、等腰三角形的判定、相似三角形的判定与性质、等腰直角三角形的判定与性质等知识;本题综合性强,难度较大,特别是(2)中,需要证明三角形相似得出比例式才能得出结果.

练习册系列答案
相关题目
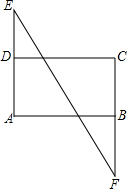 如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由.
如图,已知∠E=∠F,∠A=∠C,探求AB与CD的位置关系,并说明理由. 如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推.
如图,已知△A1BC中,∠A1=64°,BA2平分∠A1BC,CA2平分∠A1CE,BA2、CA2相交于A2;BA3平分∠A2BC,CA3平分∠A2CE,BA3、CA3相交于A3,依此类推. 已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.
已知:如图,∠ABC+∠C+∠CDE=360°,GH分别交AB、ED于点G、H,求证:∠1=∠2.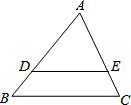 如图,已知DE∥BC,AD=5,DB=3,DE=4,则BC=$\frac{32}{5}$.
如图,已知DE∥BC,AD=5,DB=3,DE=4,则BC=$\frac{32}{5}$.