题目内容
14．
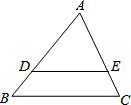如图，已知DE∥BC，AD=5，DB=3，DE=4，则BC=$\frac{32}{5}$．
分析 根据“平行线法”证得△ADE∽△ABC，则由相似三角形的对应边成比例得到$\frac{AD}{AB}$=$\frac{DE}{BC}$，把相关线段的长度代入即可求得BC的值．
解答 解：如图，∵AD=5，DB=3，
∴AB=AD+DB=8
∵DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$，即$\frac{5}{8}$=$\frac{4}{BC}$，
解得BC=$\frac{32}{5}$．
故答案是：$\frac{32}{5}$．
点评 本题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
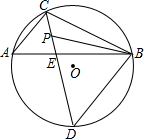已知，如图，AB为直径，△ABC内接于⊙O，点P是△ABC的内心，延长CP交圆于点D，连接BP．
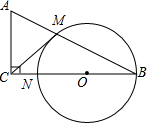如图：在△ABC中，∠ACB=90°，以BC上一点O为圆心，以OB为半径的圆交AB于点M，交BC于点N．
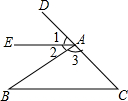如图，∠1与∠C是两条直线AE、BC被第三条直线CD所截构成的同位角；∠2与∠B是两条直线AE、BC被第三条直线CD所截构成的内错角；∠B与∠C是AB、AC被第三条直线BC所截构成的同旁内角．
9．若二次函数y=7x2-7x+m的图象与x轴有交点，则m的取值范围是（ ）
| A． | m$＞\frac{7}{4}$ | B． | m$≥\frac{7}{4}$ | C． | m$＜\frac{7}{4}$ | D． | m$≤\frac{7}{4}$ |
19．在平面直角坐标系xOy中，点A的坐标为（4，3），将线段OA绕原点O顺时针旋转180°，得到OA′，则点A′的坐标是（ ）
| A． | （-4，3） | B． | （-3，4） | C． | （3，-4） | D． | （-4，-3） |
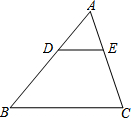如图，在△ABC中，D为AB边上一点，DE∥BC交AC于点E．若$\frac{AD}{BD}$=$\frac{2}{3}$，DE=6，则BC的长为15．