题目内容
10．
如图，已知：在△ABC中，∠B=60°，∠BAC=70°，AD⊥BC于D，∠CAD=40°．
分析 先根据三角形的内角和得出∠C=50°，再利用直角三角形的两锐角互余即可得出结论．
解答 解：在△ABC中，∠B=60°，∠BAC=70°，
∴∠C=180°-（∠B+∠BAC）=50°，
∵AD⊥BC，
∴∠ADC=90°，
在Rt△ACD中，∠CAD=90°-∠C=40°；
故答案为：40°．
点评 此题是三角形内角和定理，主要考查了三角形内角和定理，垂直的定义，直角三角形的性质，得出△ACD是直角是解本题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
12．有理数a等于它的倒数，有理数b等于它的相反数，则a2017+b2017的值是（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | ±1 |
13．
如图，已知△ABC的高AD，角平分线AE，∠B=24°，∠ACD=56°，那么∠AED的度数是（ ）
如图，已知△ABC的高AD，角平分线AE，∠B=24°，∠ACD=56°，那么∠AED的度数是（ ）| A． | 45° | B． | 42° | C． | 41° | D． | 40° |
10．若式子m$\sqrt{-\frac{1}{m}}$有意义，则化简此式等于（ ）
| A． | $\sqrt{m}$ | B． | $\sqrt{-m}$ | C． | -$\sqrt{m}$ | D． | -$\sqrt{-m}$ |
5．一个圆柱的底面半径为Rcm，高为8cm，若它的高不变，将底面半径增加了2cm，体积相应增加了192πcm，则R=（ ）
| A． | 4cm | B． | 5cm | C． | 6cm | D． | 7cm |
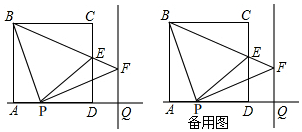
如图，∠ADC=∠ABC=90°，AD=AB，E是AB上任意一点．求证：DE=BE．
