题目内容
1.关于x的一元二次方程(a-5)x2-4x-1=0有实数根,则a满足( )| A. | a≥1 | B. | a>1且a≠5 | C. | a≥1且a≠5 | D. | a≠5 |
分析 由方程有实数根可知根的判别式b2-4ac≥0,结合二次项的系数非零,可得出关于a一元一次不等式组,解不等式组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{a-5≠0}\\{(-4)^{2}-4×(a-5)×(-1)≥0}\end{array}\right.$,
解得:a≥1且a≠5.
故选C.
点评 本题考查了根的判别式,解题的关键是得出关于a的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,由根的判别式结合二次项系数非零得出不等式组是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
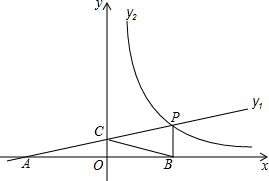 如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.
如图所示,直线y1=$\frac{1}{4}x+1$与x轴交于点A,与y轴交于点C,与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于点P,作PB⊥x轴于点B,且AC=BC.