题目内容
6.若关于x的不等式-mx-n>0的解集是x$>\frac{1}{5}$,则关于x的不等式(m-n)x>n+m的解集是x<$\frac{2}{3}$.分析 先解关于x的不等式-mx-n>0,得出解集,再根据不等式的解集是x$>\frac{1}{5}$,从而得出m与n的关系,解得即可.
解答 解:∵关于x的不等式-mx-n>0的解集是x$>\frac{1}{5}$,
∴m<0,-$\frac{n}{m}$=$\frac{1}{5}$,
解得m=-5n,
∴n>0,
∴解关于x的不等式(m-n)x>n+m得,x<$\frac{n+m}{m-n}$,
∴x<$\frac{n-5n}{-5n-n}$=$\frac{2}{3}$,
故答案为x<$\frac{2}{3}$.
点评 本题考查了不等式的解集以及不等式的性质,要熟练掌握不等式的性质3.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
1.关于x的一元二次方程(a-5)x2-4x-1=0有实数根,则a满足( )
| A. | a≥1 | B. | a>1且a≠5 | C. | a≥1且a≠5 | D. | a≠5 |
11.实数$\sqrt{17}$在哪两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |
18.如果一个实数的算术平方根等于它的立方根,那么满足条件的实数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
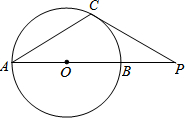 如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,若AB=8,∠CPA=30°,则PC的长等于4$\sqrt{3}$.
如图,AB是⊙O的直径,点P在AB的延长线上,PC切⊙O于点C,若AB=8,∠CPA=30°,则PC的长等于4$\sqrt{3}$.