题目内容
如图(1)是长方形纸带,∠DEF=m,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE度数 (用含m的代数式表示).


考点:翻折变换(折叠问题)
专题:
分析:如图1,证明∠CFE=180°-m.此为解决该题的关键性结论;证明∠CFG=180°-2m,进而证明,∠CFE=180°-3m,即可解决问题.
解答: 解:如图1,∵四边形ABCD为矩形,
解:如图1,∵四边形ABCD为矩形,
∴DE∥CF,
∴∠DEF+∠CFE=180°
∴∠CFE=180°-m.
如图2,∵∠EFG=∠DEF=m,
∴∠CFG=180°-2m.
如图3,∠CFE=∠CFG-∠EFG=180°-3m.
故答案为180°-3m.
 解:如图1,∵四边形ABCD为矩形,
解:如图1,∵四边形ABCD为矩形,∴DE∥CF,
∴∠DEF+∠CFE=180°
∴∠CFE=180°-m.
如图2,∵∠EFG=∠DEF=m,
∴∠CFG=180°-2m.
如图3,∠CFE=∠CFG-∠EFG=180°-3m.
故答案为180°-3m.
点评:该题以矩形为载体,以翻折变换为方法,以平行线的性质等几何知识点为考查的核心构造而成;在图2、图3中,∠CFG的大小始终不变,这是解题的关键.

练习册系列答案
相关题目
已知(a-1)2+
=0,则
+
+
+…+
值是( )
| b-2 |
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2015)(b+2015) |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
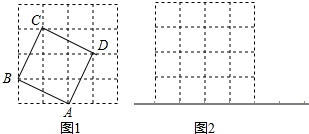 如图,4×4方格中每个小正方形的边长都为1.
如图,4×4方格中每个小正方形的边长都为1. 如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由.
如图,⊙O是△ABC的内切圆,D、E、F分别是切点,判定△DEF的形状(按角分类),并说明理由.