题目内容
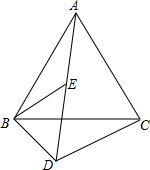 已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明
已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明DA-DB=DC.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质,可得AB与BC的关系,BD、BE、DE的关系,根据三角形全等的判定,可得△ABE与△CBD的关系,根据全等三角形的性质,可得对应边相等,根据线段的和差,等量代换,可得证明结果.
解答:证明:△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD=DE(等边三角形的边相等),
∠ABC=∠EBD=60°(等边三角形的角是60°).
∴∠ABC-∠EBC=∠EBD-∠EBC
∠ABE=CBD (等式的性质),
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS)
∴AE=DC(全等三角形的对应边相等).
∵AD-DE=AE(线段的和差)
∴AD-BD=DC(等量代换).
∴AB=BC,BE=BD=DE(等边三角形的边相等),
∠ABC=∠EBD=60°(等边三角形的角是60°).
∴∠ABC-∠EBC=∠EBD-∠EBC
∠ABE=CBD (等式的性质),
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS)
∴AE=DC(全等三角形的对应边相等).
∵AD-DE=AE(线段的和差)
∴AD-BD=DC(等量代换).
点评:本题考查了全等三角形的判定与性质,先证明三角形全等,再证明全等三角形的对应边相等,最后等量代换.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
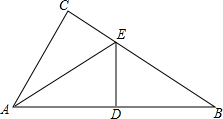 如图,△ABC中,∠C=90°,AC=6,BC=8,现将△ABC沿着DE折叠,使点B与点A重合,则tan∠CAE的值是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,现将△ABC沿着DE折叠,使点B与点A重合,则tan∠CAE的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF=
如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF=
 已知一次函数y=-x+1与抛物线y=
已知一次函数y=-x+1与抛物线y=