题目内容
解下列方程组
(1)
;
(2)
;
(3)
;
(4)
.
(1)
|
(2)
|
(3)
|
(4)
|
考点:解二元一次方程组
专题:计算题
分析:(1)利用代入消元法求出解即可;
(2)利用加减消元法求出解即可;
(3)方程组整理后,利用代入消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
(2)利用加减消元法求出解即可;
(3)方程组整理后,利用代入消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答:解:(1)
,
①代入②得:3x+4x-6=1,
解得:x=1,
将x=1代入①得:y=-1,
则方程组的解为
;
(2)
,
①×2+②得:11x=11,即x=1,
将x=1代入①得:4+y=5,即y=1,
则方程组的解为
;
(3)方程组整理得:
,
①代入②得:2y+y=18,即y=6,
将y=6代入①得:x=4,
则方程组的解为
;
(4)
,
①×3+②×4得:17y=204,即y=12,
将y=12代入②得:x=9,
则方程组的解为
.
|
①代入②得:3x+4x-6=1,
解得:x=1,
将x=1代入①得:y=-1,
则方程组的解为
|
(2)
|
①×2+②得:11x=11,即x=1,
将x=1代入①得:4+y=5,即y=1,
则方程组的解为
|
(3)方程组整理得:
|
①代入②得:2y+y=18,即y=6,
将y=6代入①得:x=4,
则方程组的解为
|
(4)
|
①×3+②×4得:17y=204,即y=12,
将y=12代入②得:x=9,
则方程组的解为
|
点评:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
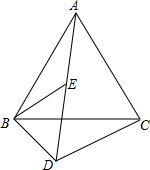 已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明
已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明
 如图,△ABC是等边三角形,D、E分别是BC、AC上的点,BD=CE,求∠AFE的度数.
如图,△ABC是等边三角形,D、E分别是BC、AC上的点,BD=CE,求∠AFE的度数. 如图,添上
如图,添上