Question

已知：正方形ABCD的边长为4，点E为BC的中点，点P为AB上一动点，沿PE翻折△BPE得到△FPE，直线PF交CD边于点Q，交直线AD于点G，联接EQ．

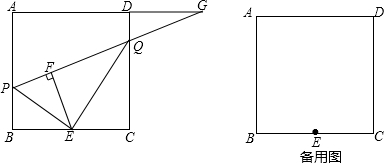
（1）如图，当BP=1.5时，求CQ的长；
（2）如图，当点G在射线AD上时，BP=x，DG=y，求y关于x的函数关系式，并写出x的取值范围；
（3）延长EF交直线AD于点H，若△CQE与△FHG相似，求BP的长．

Answer 1

考点：相似形综合题

专题：

分析：（1）首先确定∠PEQ=90°，即PE⊥EQ，然后利用△PBE∽△ECQ，列出比例式求出CD的长度；
（2）根据△PBE∽△ECQ，求出DQ的表达式；由QD∥AP，列出比例式求解；
（3）本问分两种情形，需要分类讨论，避免漏解．

解答：解：（1）由翻折性质，可知PE为∠BPQ的角平分线，且BE=FE．
∵点E为BC中点，
∴EC=EB=EF，
∴QE为∠CQP的角平分线．
∵AB∥CD，
∴∠BPQ+∠CQP=180°，即2∠EPQ+2∠EQP=180°，
∴∠EPQ+∠EQP=90°，
∴∠PEQ=90°，即PE⊥EQ．
易证△PBE∽△ECQ，
∴

BP

EC

=

BE

CQ

，即

1.5

2

=

2

CQ

，
解得：CQ=

8

3

．

（2）由（1）知△PBE∽△ECQ，
∴

BP

EC

=

BE

CQ

，即

x

2

=

2

CQ

，
∴CQ=

4

x

，∴DQ=4-

4

x

．
∵QD∥AP，∴

DG

AG

=

DQ

AP

，又AP=4-x，AG=4+y，
∴

y

4+y

=

4- 4 x

4-x

，
∴y=

16x-16

4-x2

（1＜x＜2）．

（3）由题意知：∠C=90°=∠GFH．
①当点G在线段AD的延长线上时，如答图1所示．
由题意知：∠G=∠CQE
∵∠CQE=∠FQE，
∴∠DQG=∠FQC=2∠CQE=2∠G．
∵∠DQG+∠G=90°，
∴∠G=30°，
∴∠BEP=∠CQE=∠G=30°，
∴BP=BE•tan30°=

2

3

3

；

②当点G在线段DA的延长线上时，如答图2所示．
由题意知：∠FHG=∠CQE．
同理可得：∠G=30°，
∴∠BPE=∠G=30°，
∴∠BEP=60°，
∴BP=BE•tan60°=2

3

．
综上所述，BP的长为

2

3

3

或2

3

．

点评：本题是几何综合题型，主要考查了相似三角形、正方形、解直角三角形、角平分线等几何知识点．难点在于第（3）问，有两种情形，不要漏解．