题目内容
 已知一次函数y=-x+1与抛物线y=
已知一次函数y=-x+1与抛物线y=| 1 |
| 3 |
(1)求b,c的值;
(2)判断△ABC的形状并说明理由;
(3)点D、E分别为线段AB、BC上任意一点,连接CD,取CD的中点F,连接AF,EF.当四边形ADEF为平行四边形时,求平行四边形ADEF的周长.
考点:二次函数综合题
专题:
分析:(1)把A坐标代入抛物线解析式可求出c的值,把B的纵坐标代入直线解析式可求出其横坐标,再代入抛物线解析式即可求出b的值;
(2)△ABC的形状是直角三角形,分别作BG垂直于y轴,CH垂直于y轴,依次求∠BAG=45°,∠CAH=45°,进而得到∠BAC=90°;
(3)首先利用勾股定理易求AB的长,进而得到AC的长,利用三角形中位线的性质即可求出EF的长,再利用勾股定理即可求出AF的长,继而求出平行四边形ADEF的周长.
(2)△ABC的形状是直角三角形,分别作BG垂直于y轴,CH垂直于y轴,依次求∠BAG=45°,∠CAH=45°,进而得到∠BAC=90°;
(3)首先利用勾股定理易求AB的长,进而得到AC的长,利用三角形中位线的性质即可求出EF的长,再利用勾股定理即可求出AF的长,继而求出平行四边形ADEF的周长.
解答:解:(1)把A(0,1),代入y=
x2+bx+c,
解得c=1,
将y=10代入y=-x+1,得x=-9,
∴B点坐标为(-9,10),
将B (-9,10),代入y=
x2+bx+c
得b=2;
(2)△ABC是直角三角形,
理由如下:
∵y=
x2+2x+1=
(x+3)2-2,
∴点C的坐标为(-3,-2),
分别作BG垂直于y轴,CH垂直于y轴
∵B=AG=9,
∴∠BAG=45°,
同理∠CAH=45°,
∴∠CAB=45°
∴△ABC是直角三角形;
(3)∵BG=AG=9,
∴AB=9
,
∵CH=AH=3,
∴AC=3
,
∵四边形ADEF为平行四边形,
∴AD∥EF,
又∵F为CD中点,
∴CE=BE,
即EF为△DBC的中位线,EF
∴EF=AD=
BD,
∵AB=9
,
∴EF=AD=3
在Rt△ACD中,AD=3
,CD=3
,
∴CD=6,
∴AF=3,
∴平行四边形ADEF周长为6+6
.
| 1 |
| 3 |
解得c=1,
将y=10代入y=-x+1,得x=-9,
∴B点坐标为(-9,10),
将B (-9,10),代入y=
| 1 |
| 3 |
得b=2;
(2)△ABC是直角三角形,
理由如下:

∵y=
| 1 |
| 3 |
| 1 |
| 3 |
∴点C的坐标为(-3,-2),
分别作BG垂直于y轴,CH垂直于y轴
∵B=AG=9,
∴∠BAG=45°,
同理∠CAH=45°,
∴∠CAB=45°
∴△ABC是直角三角形;
(3)∵BG=AG=9,
∴AB=9
| 2 |
∵CH=AH=3,
∴AC=3
| 2 |
∵四边形ADEF为平行四边形,
∴AD∥EF,
又∵F为CD中点,
∴CE=BE,
即EF为△DBC的中位线,EF
∴EF=AD=
| 1 |
| 2 |
∵AB=9
| 2 |
∴EF=AD=3
| 2 |
在Rt△ACD中,AD=3
| 2 |
| 2 |
∴CD=6,
∴AF=3,
∴平行四边形ADEF周长为6+6
| 2 |
点评:本题主要考查了二次函数解析式的确定、二次函数的性质、勾股定理的运用、直角三角形的判定方法和性质、三角形中位线定理、平行四边形的性质和平行三边的周长计算,题目的综合性较强,难度中等.

练习册系列答案
相关题目
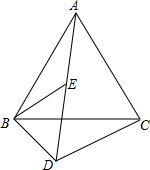 已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明
已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明 如图,直线AB、CD相交于点O,OE平分∠AOB,OB平分∠DOF,若∠DOE=50°,求∠DOF的度数.
如图,直线AB、CD相交于点O,OE平分∠AOB,OB平分∠DOF,若∠DOE=50°,求∠DOF的度数.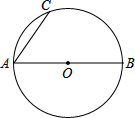 如图,AB是⊙O的直径,AC是弦.
如图,AB是⊙O的直径,AC是弦.
 如图,添上
如图,添上