题目内容
 如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF=
如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF=| 1 |
| 2 |
考点:线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:连接AF,根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°,根据线段的垂直平分线的性质得出BF=AF,推出∠BAF=∠B=30°,求出∠FAC=90°,根据含30度角的直角三角形性质求出即可.
解答: 证明:连接AF,
证明:连接AF,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴BF=AF,
∴∠BAF=∠B=30°,
∴∠FAC=120°-30°=90°,
∵∠C=30°,
∴AF=
CF,
∵BF=AF,
∴BF=
FC.
 证明:连接AF,
证明:连接AF,∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵EF为AB的垂直平分线,
∴BF=AF,
∴∠BAF=∠B=30°,
∴∠FAC=120°-30°=90°,
∵∠C=30°,
∴AF=
| 1 |
| 2 |
∵BF=AF,
∴BF=
| 1 |
| 2 |
点评:本题考查了线段垂直平分线,等腰三角形性质,三角形内角和定理,含30度角的直角三角形性质的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
已知一组数据x1,x2,x3的平均数和方差分别为6和2,则数据x1+1,x2+1,x3+1的平均数和方差分别是( )
| A、6和2 | B、6和3 |
| C、7和2 | D、7和3. |
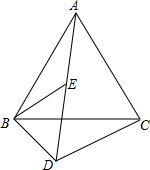 已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明
已知:如图,△ABC和△BDE都是等边三角形,且A,E,D三点在一直线上.请你说明