题目内容
15.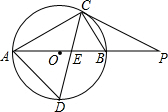 如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.(1)求AC,AD的长.
(2)廷长AB至点P,连接PC,当BP等于多少时,PC与⊙O相切?为什么?
分析 (1)连接BD,在Rt△ABC中,可求得AB、AC,又可知△ABD为等腰直角三角形,可求得AD;
(2)连接OC,可先证明△OBC为等边三角形,当PC为切线时,可求得BP=BC,可得出结论.
解答 解:
(1)如图1,连接BD,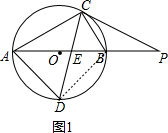
∵AB是直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵∠CAB=30°,BC=1,
∴AB=2,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵CD平分∠ACB,
∴△ABD为等腰直角三角形,
∴AD=BD=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$;
(2)如图2,连接OC,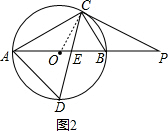
∵∠CAB=30°,
∴∠COB=60°,
∴△OBC为等边三角形,
当PC为⊙O的切线时,则∠OCP=90°,
∴∠BCP=∠BPC=30°,
∴PB=BC=1,
即当PB=1时,PC与⊙O相切.
点评 本题主要考查切线判定和性质及解直角三角形,掌握切线的判定方法是解题的关键,即有切点时连接圆心和切点,然后证明垂直,没有切点时,过圆心作垂直,证明圆心到直线的距离等于半径.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3.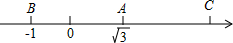 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
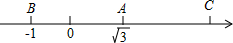 如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )
如图,数轴上A、B两点对应的实数是$\sqrt{3}$和-1,AC=AB,则点C所对应的实数是( )| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{3}$+1 |
10.下列图案中既是轴对称又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.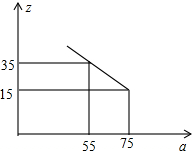 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系,求z与a之间的函数关系式.
(3)若该厂第一个月生产这种机器50台,且第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
 某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂投入生产一种机器,当该机器生产数量至少10台,但不超过70台,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系,求z与a之间的函数关系式.
(3)若该厂第一个月生产这种机器50台,且第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
7.如图1,在矩形ABCD中,AC、BD交于点O,点P在边AD上运动,PM⊥AC于点M,PN⊥BD于点N.设PM=x,PN=y,且y与x满足一次函数关系,其图象如图2所示,其中a=6,以下判断中,不正确的是( )


| A. | Rt△ABD中斜边BD上的高为6 | |
| B. | 无论点P在AD上何处,PM与PN的和始终保持不变 | |
| C. | 当x=3时,OP垂直平分AD | |
| D. | 若AD=10,则矩形ABCD的面积为60 |
 如图所示,BE平分∠ABC,DE∥BC,观察图中相等的角共有多少对?请你把它们都写出来.(用∠x=∠y的形式写具体)
如图所示,BE平分∠ABC,DE∥BC,观察图中相等的角共有多少对?请你把它们都写出来.(用∠x=∠y的形式写具体)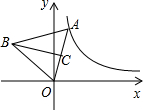 如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.
如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.