题目内容
4.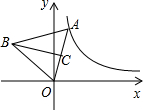 如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.
如图,在平面直角坐标系中,点A是双曲线y=$\frac{4}{x}$(x>0)上一动点,以OA为边作等边△AOB,高BC的最小值为$\sqrt{6}$.
分析 直接利用反比例函数图象上点的坐标特征得出AO的最小值,进而得出BC的最小值.
解答 解:设A点横坐标为:x,则纵坐标为:$\frac{4}{x}$,
故AO=$\sqrt{{x}^{2}+\frac{16}{{x}^{2}}}$≥2$\sqrt{{x}^{2}×\frac{16}{{x}^{2}}}$,
故$\sqrt{{x}^{2}+\frac{16}{{x}^{2}}}$≥8,
当x=2时AO最小,则AO=2$\sqrt{2}$,
故等边三角形AOB的高BC的最小值为:2$\sqrt{2}$×sin60°=2$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 此题主要考查了反比例函数图象上点的坐标特征以及等边三角形的性质,正确得出AO的最小值是解题关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
16.甲看乙的方向是北偏东30°,则乙看甲的方向是( )
| A. | 南偏东60° | B. | 南偏东30° | C. | 南偏西60° | D. | 南偏西30° |
 小刚同学把一个含有45°角的直角三角板放在如图所示的两条平行线m,n上,测得∠α=110°,则∠β的度数是65°.
小刚同学把一个含有45°角的直角三角板放在如图所示的两条平行线m,n上,测得∠α=110°,则∠β的度数是65°.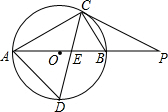 如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
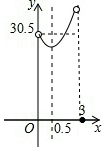
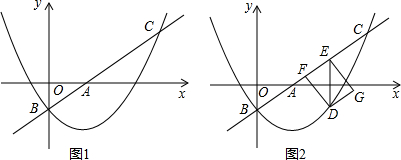
如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )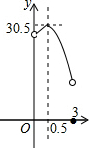
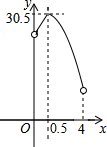





 如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.