题目内容
5.已知二元一次方程组$\left\{\begin{array}{l}{ax+by=151}\\{ay+bx=149}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=49}\\{y=51}\end{array}\right.$,则a-b的值是-1.分析 根据二元一次方程组$\left\{\begin{array}{l}{ax+by=151}\\{ay+bx=149}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=49}\\{y=51}\end{array}\right.$,代入即可得到关于a、b的二元一次方程组,通过观察,两个方程作差即可得到a-b的值.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}{ax+by=151}\\{ay+bx=149}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=49}\\{y=51}\end{array}\right.$,
∴$\left\{\begin{array}{l}{49a+51b=151}&{①}\\{51a+49b=149}&{②}\end{array}\right.$
②-①,得
2a-2b=-2,
∴a-b=-1,
故答案为:-1.
点评 本题考查二元一次方程组的解,解题的关键是明确二元一次方程组的解一定适合原二元一次方程组,将所求式子与已知条件建立关系.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.甲看乙的方向是北偏东30°,则乙看甲的方向是( )
| A. | 南偏东60° | B. | 南偏东30° | C. | 南偏西60° | D. | 南偏西30° |
17.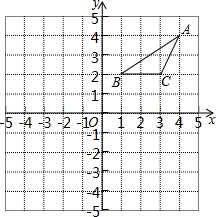 如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
 如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )| A. | A′(4,-4) | B. | B′(-1,2) | C. | A″(-4,-4) | D. | C″(-2,-1) |
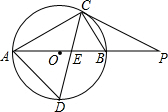 如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
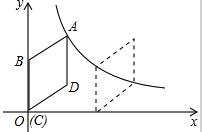 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$. 如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$.
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是$\sqrt{2}$≤AC≤3$\sqrt{2}$. 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点(-1,3),则b的值是5.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点(-1,3),则b的值是5.