题目内容
7.如图1,在矩形ABCD中,AC、BD交于点O,点P在边AD上运动,PM⊥AC于点M,PN⊥BD于点N.设PM=x,PN=y,且y与x满足一次函数关系,其图象如图2所示,其中a=6,以下判断中,不正确的是( )
| A. | Rt△ABD中斜边BD上的高为6 | |
| B. | 无论点P在AD上何处,PM与PN的和始终保持不变 | |
| C. | 当x=3时,OP垂直平分AD | |
| D. | 若AD=10,则矩形ABCD的面积为60 |
分析 (A)根据图②中的信息求得y的最大值,即可得出Rt△ABD中斜边BD上的高;
(B)根据图②中的信息可得,y与x满足一次函数关系,x与y的和为定值;
(C)先判断P为AD的中点,再根据等腰三角形AOD三线合一即可得出结论;
(D)先根据勾股定理求得DE,再利用射影定理求得BE,最后根据矩形的面积等于△ABD面积的2倍进行计算即可.
解答 解:(A)由图②可得,x+y=6,所以当x=0时,y=6,即PN的最大值为6,所以Rt△ABD中斜边BD上的高AE为6,故(A)正确;
(B)由图②可得,x+y=6,所以无论点P在AD上何处,PM与PN的和始终为6,故(B)正确;
(C)当x=3时,y=3,此时PN=PM,易得△APM≌△DPN,所以点P为AD的中点,所以等腰三角形AOD中,OP垂直平分AD,故(C)正确;
(D)若AD=10,则直角三角形ADE中,DE=$\sqrt{1{0}^{2}-{6}^{2}}$=8,由射影定理可得BE=$\frac{A{E}^{2}}{DE}$=$\frac{9}{2}$,所以矩形ABCD的面积=2×$\frac{1}{2}$×($\frac{9}{2}$+8)×6=75,故(D)错误.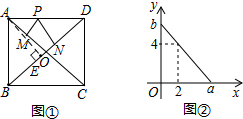
点评 本题以动点问题为背景考查了矩形的性质与一次函数的图象,判断PM+PN的值是定值是解决问题的关键,解题时注意:图①中,根据面积法可得PM+PN=AE.

练习册系列答案
相关题目
17.计算1252016×(-0.008)2015的结果为( )
| A. | -$\frac{1}{125}$ | B. | -125 | C. | $\frac{1}{125}$ | D. | 125 |
16.甲看乙的方向是北偏东30°,则乙看甲的方向是( )
| A. | 南偏东60° | B. | 南偏东30° | C. | 南偏西60° | D. | 南偏西30° |
17.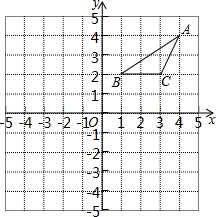 如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
 如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )
如图,△ABC顶点的坐标分别是A(4,4),B(1,2),C(3,2),现将△ABC绕原点O逆时针方向旋转90°得到△A′B′C′,再将△A′B′C′向下平移4个单位长度得到△A″B″C″,则下列点的坐标正确的是( )| A. | A′(4,-4) | B. | B′(-1,2) | C. | A″(-4,-4) | D. | C″(-2,-1) |
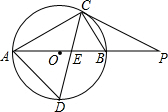 如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.
如图,⊙O是△ABC的外接圆,AB是直径,∠CAB=30°,BC=1,∠ACB的平分线交⊙O于点D,交AB于点E.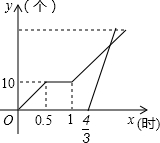 某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象
某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同.其中的一个小正方形ABCD如图乙所示,DG=1米,AE=AF=x米,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )