题目内容
假设三边长、周长、面积都为整数的三角形叫做“整数三角形”,请写出所有周长为32的“钝角整数三角形”,分别列出它的三边长.
考点:三角形边角关系
专题:探究型
分析:设周长为32的“钝角整数三角形”的三边长分别为a、b、c,不妨设a>b≥c,则有a、b、c为正整数,a<b+c,a+b+c=32,a2>b2+c2,S=
是整数.根据三角形的构成条件可以确定a的范围,然后分类讨论就可解决问题.
| 16(16-a)(16-b)(16-c) |
解答:解:设周长为32的“钝角整数三角形”的三边长分别为a、b、c,
不妨设a>b≥c,则有a、b、c为正整数,a<b+c,a+b+c=32,
a2>b2+c2,S=
是整数.
∵a<b+c,a+b+c=32,
∴2a<a+b+c=32,
∴a<16.
∵a>b≥c,a、b、c为正整数,
∴a≥b+1,a≥c+1,
∴3a≥a+b+1+c+1=34,
∴a≥
,
∴
≤a<16,
∴整数a可取15、14、13、12.
①当a=15时,可得:
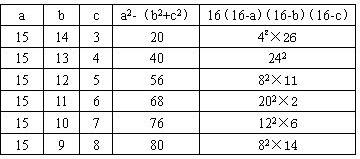
由上表可知:三边长为15,13,4时符合要求.
②当a=14时,可得:
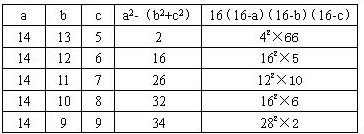
由上表可知:三角形面积都不是整数,因而都不符合要求.
③当a=13时,可得:
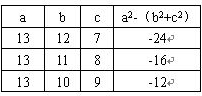
由上表可知:三角形都是锐角三角形,都不符合要求.
④当a=12时,可得:
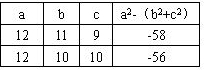
由上表可知:三角形都是锐角三角形,都不符合要求.
综上所述:周长为32的“钝角整数三角形”只有一个,它的三边长分别为15、13、4.
不妨设a>b≥c,则有a、b、c为正整数,a<b+c,a+b+c=32,
a2>b2+c2,S=
| 16(16-a)(16-b)(16-c) |
∵a<b+c,a+b+c=32,
∴2a<a+b+c=32,
∴a<16.
∵a>b≥c,a、b、c为正整数,
∴a≥b+1,a≥c+1,
∴3a≥a+b+1+c+1=34,
∴a≥
| 34 |
| 3 |
∴
| 34 |
| 3 |
∴整数a可取15、14、13、12.
①当a=15时,可得:

由上表可知:三边长为15,13,4时符合要求.
②当a=14时,可得:

由上表可知:三角形面积都不是整数,因而都不符合要求.
③当a=13时,可得:

由上表可知:三角形都是锐角三角形,都不符合要求.
④当a=12时,可得:

由上表可知:三角形都是锐角三角形,都不符合要求.
综上所述:周长为32的“钝角整数三角形”只有一个,它的三边长分别为15、13、4.
点评:本题主要考查了三角形的三边关系(两边之和大于第三边)、钝角三角形的判定方法(最长边的平方大于其它两边的平方和)、海伦公式(S=
,其中p=
),有一定的难度,而运用分类讨论及枚举法则是解决本题的关键.
| p(p-a)(p-b)(p-c) |
| a+b+c |
| 2 |

练习册系列答案
相关题目
设完全平方数M的个位与十位数码交换后得到另一个完全平方数N(M>N).则符合条件的M的个数为( )
| A、1 | B、2 | C、3 | D、多于3 |
 已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°-
已知PA、PB切⊙O于点A、B,过弧AB上任一点E作⊙O的切线,交PA、PB于点C、D,试证明:∠COD=90°- 已知y+2与x成正比例,且x=-2时,y=0.
已知y+2与x成正比例,且x=-2时,y=0. 如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.
如图,△ABC中,∠ACB=120°,∠A=20°,CD⊥AB于D,试探究BC、BD、AD之间的关系.