题目内容
设完全平方数M的个位与十位数码交换后得到另一个完全平方数N(M>N).则符合条件的M的个数为( )
| A、1 | B、2 | C、3 | D、多于3 |
考点:完全平方数
专题:
分析:可设原来完全平方数M的个位数码是a,十位数码是b,则交换后得到另一个完全平方数N的个位数码是b,十位数码是a,因为M>N,所以两个数的差是(10b+a)-(10a+b)=9(b-a),依此根据平方差公式讨论求解.
解答:解:设原来完全平方数M的个位数码是a,十位数码是b,则交换后得到另一个完全平方数N的个位数码是b,十位数码是a,
因为M>N,
所以两个数的差是(10b+a)-(10a+b)=9(b-a),
设M=x2,N=y2,
则M-N=x2-y2=(x+y)(x-y)=9(b-a),
由于完全平方数个位上只能是0(不合题意),1,4,5,6,9,
则b-a=1,2,3,4,5,8,9,
则有
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
,解得
,即M=196,N=169(符合题意),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去),
(不合题意舍去).
只有一组解符合要求,因此符合条件的M是196,个数为1.
故选:A.
因为M>N,
所以两个数的差是(10b+a)-(10a+b)=9(b-a),
设M=x2,N=y2,
则M-N=x2-y2=(x+y)(x-y)=9(b-a),
由于完全平方数个位上只能是0(不合题意),1,4,5,6,9,
则b-a=1,2,3,4,5,8,9,
则有
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
只有一组解符合要求,因此符合条件的M是196,个数为1.
故选:A.
点评:本题考查了完全平方数与整数的十进制表示法,关键是设出原来完全平方数M的个位数码是a,十位数码是b,然后根据题意列方程求解.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
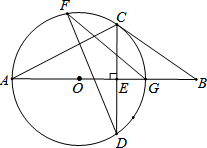 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
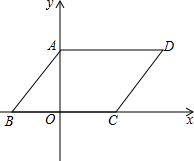 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.