题目内容
若直线y1=-2x1+a与y2=3x2-b相交于点(-4,c),则要使y1>y2成立.则自变量x的范围为 .
考点:一次函数与一元一次不等式
专题:
分析:直线y1在直线y2上方的部分对应的x的取值范围即为所求.
解答:解:∵直线y1=-2x1+a与y2=3x2-b相交于点(-4,c),
∴要使y1>y2成立,则自变量x的范围为x<-4.
故答案为x<-4.
∴要使y1>y2成立,则自变量x的范围为x<-4.
故答案为x<-4.
点评:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
若一元二次方程(m-1)x2+(m2+1)x+m2-1=0的常数项为0,则m的值为( )
| A、1 | B、-1 | C、±1 | D、0 |
 如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.
如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.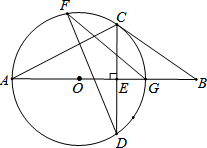 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.