题目内容
1.某服装店老板以50元的价格购进20件T恤衫,这20件T恤衫的市场售价不完全相同.若以60元的售价为标准,将超过的钱数记为正,不足的钱数记为负,销售结果记录如下:| 与60元的售价偏差(元) | -15 | -12 | -8 | 0 | +4 | +5 | +7 |
| 件数(件) | 1 | 3 | 5 | 4 | 4 | 2 | 1 |
(2)该服装店在售完这20件T恤衫后,赚了多少元钱.
分析 (1)由加价最多的就是赚钱最多的T恤,由此比较,进一步计算得出答案即可;
(2)首先由进货量和每件的利润得出价格不变的总利润,然后再根据利润变化计算出多或少的利润,求和得出赚了多少钱即可.
解答 解:(1)60+7-50=17(元)
答:这20件中赚钱最多的T恤衫赚了17元钱;
(2)由题意得
(60-50)×20-15-12×3-8×5+0×4+4×4+5×2+7×1
=200-15-36-40+16+10+7
=142(元).
答:该服装店在售完这20件T恤衫后,赚了142元钱.
点评 本题主要考查正负数的意义,有理数的混合运算,关键在于理解表格中的数值是以60为标准.

练习册系列答案
相关题目
6.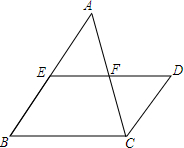 如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
 如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )
如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( )| A. | 相等 | B. | 平行 | C. | 平行且相等 | D. | 以上都不是 |
11.“十一”节期间,某商品按成本价提高30%后标价,再打8折(标价的80%)销售,售价为240元.设该商品的成本价为x元,根据题意,下面所列方程正确的是( )
| A. | x•30%•80%=240 | B. | x•(1+30%)•80%=240 | ||
| C. | x•(1+30%)•(1-80%)=240 | D. | x•30%=240•80% |
 如图,点A、B、C在⊙O上,D是$\widehat{AB}$的中点,CD交OB于点E,若∠AOB=100°,∠OBC=55°,求∠OEC的度数.
如图,点A、B、C在⊙O上,D是$\widehat{AB}$的中点,CD交OB于点E,若∠AOB=100°,∠OBC=55°,求∠OEC的度数.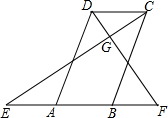 已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.
已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.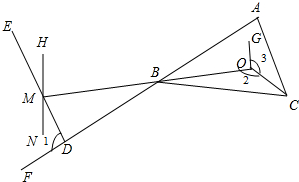 已知:如图,点D在射线AF上,AF与OM交于点B,DE交NH于点M,CA∥DE.
已知:如图,点D在射线AF上,AF与OM交于点B,DE交NH于点M,CA∥DE.