题目内容
9.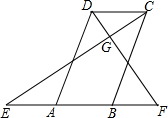 已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.
已知,如图,在四边形ABCD中,AD∥BC,点E、F分别是BA、AB延长线上的点,且满足:∠ADF=∠F,∠BCE=∠E,EC、DF交于点G.(1)试猜想∠F和∠DAF之间有怎样的数量关系;
(2)求∠EGF的度数.
分析 (1)由三角形内角和定理和已知条件即可得出结果;
(2)证出∠2=∠F,由三角形的外角性质得出∠1=2∠E,由三角形内角和定理求出∠E+∠F=90°,即可得出∠EGF=90°.
解答 (1)解:2∠F+∠DAF=180°;理由如下:
∠ADF=∠F,∠ADF+∠F+∠DAF=180°,
∴2∠F+∠DAF=180°;
(2)解:如图所示: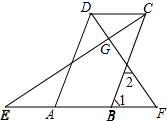
∵AD∥BC,
∴∠2=∠ADF,
∵∠ADF=∠F,
∴∠2=∠F,
∵∠1=∠BCE+∠E,∠BCE=∠E,
∴∠1=2∠E,
∵∠1+∠F+∠2=180°,
∴2∠E+2∠F=180°,
∴∠E+∠F=90°,
∴∠EGF=90°.
点评 本题考查了平行线的性质、三角形内角和定理、三角形的外角性质等知识;有一定难度.

练习册系列答案
相关题目
1.某服装店老板以50元的价格购进20件T恤衫,这20件T恤衫的市场售价不完全相同.若以60元的售价为标准,将超过的钱数记为正,不足的钱数记为负,销售结果记录如下:
(1)这20件中赚钱最多的T恤衫赚了多少元钱;
(2)该服装店在售完这20件T恤衫后,赚了多少元钱.
| 与60元的售价偏差(元) | -15 | -12 | -8 | 0 | +4 | +5 | +7 |
| 件数(件) | 1 | 3 | 5 | 4 | 4 | 2 | 1 |
(2)该服装店在售完这20件T恤衫后,赚了多少元钱.
19.如果点M(a,a+1)在x轴上,则a的值为( )
| A. | a=1 | B. | a=-1 | C. | a>0 | D. | a的值不能确定 |
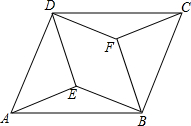 在平行四边形ABCD中,分别以AD,BC为斜边向内作等腰直角△ADE和等腰直角△BCF,连接BE,DF,求证:四边形BEDF是平行四边形.
在平行四边形ABCD中,分别以AD,BC为斜边向内作等腰直角△ADE和等腰直角△BCF,连接BE,DF,求证:四边形BEDF是平行四边形. 已知:如图,△ABC中,∠BAC=100°,在BC边上取点D,使得∠BAD=80°,∠CAD=20°,CE平分∠ACB,联结AD,DE,求∠CED的大小.
已知:如图,△ABC中,∠BAC=100°,在BC边上取点D,使得∠BAD=80°,∠CAD=20°,CE平分∠ACB,联结AD,DE,求∠CED的大小.