Question

16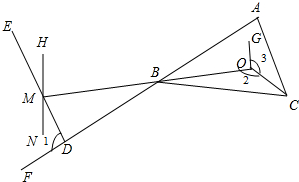．已知：如图，点D在射线AF上，AF与OM交于点B，DE交NH于点M，CA∥DE．
（1）求证：∠1=∠ABC+∠ACB；
（2）若BO平分∠ABC，CO平分∠ACB，∠1=∠BMN，∠2=∠3，求证：OG∥HN．

Answer 1

分析 （1）根据平角的定义和三角形的内角和得到∠1+∠MDB=180°，∠A=180°-（∠ABC+∠ACB），由平行线的性质得到∠MDB=∠A，即可得到；
（2）由BO平分∠ABC，CO平分∠ACB，得到∠OBC=$\frac{1}{2}∠$ABC，∠OCB=$\frac{1}{2}∠$ACB，根据三角形的内角和得到∠2=180°-∠OBC-∠OCB=180°-$\frac{1}{2}$（∠ABC+∠ACB），于是求得∠GOB=360°-∠2-∠3=360°-2[180°-$\frac{1}{2}$（∠ABC+∠ACB）]=∠ABC+∠ACB，由∠1=∠BMN=∠ACB+∠ABC，得到∠BMN=∠GOB，即可得到结论．

解答 解：（1）∵∠1+∠MDB=180°，∠A=180°-（∠ABC+∠ACB），
∵CA∥DE，
∴∠MDB=∠A，
∴∠1=∠ABC+∠ACB；

（2）∵BO平分∠ABC，CO平分∠ACB，
∴∠OBC=$\frac{1}{2}∠$ABC，∠OCB=$\frac{1}{2}∠$ACB，
∴∠2=180°-∠OBC-∠OCB=180°-$\frac{1}{2}$（∠ABC+∠ACB），
∵∠2=∠3，
∴∠GOB=360°-∠2-∠3=360°-2[180°-$\frac{1}{2}$（∠ABC+∠ACB）]=∠ABC+∠ACB，
∵∠1=∠BMN=∠ACB+∠ABC，
∴∠BMN=∠GOB，
∴OG∥HN．

点评 本题考查了平行线的判定和性质，三角形的内角和，熟练掌握平行线的判定和性质是解题的关键．