题目内容

7．设x1、x2是一元二次方程x2+5x-2013=0的两个实数根，则x1（x22+4x2-2013）的值为2013．

分析 利用根与系数的关系可得出x1+x2=-5、x1•x2=-2013，将代数式x1（x22+4x2-2013）进行转化后得出-x1•x2，再代入数据即可得出结论．

解答 解：∵x1、x2是一元二次方程x2+5x-2013=0的两个实数根，
∴x1+x2=-5，x1•x2=-2013，
∴x1（x22+4x2-2013）=x1（x22+5x2-x2-2013）=x1[x2（x2+5）-x2-2013]=x1（-x2x1-x2-2013）=x1（2013-x2-2013）=-x1•x2=2013．
故答案为：2013．

点评 本题考查了根与系数的关系，将代数式转化成-x1•x2是解题的关键．

练习册系列答案
相关题目
17．计算：
（1）$\frac{1}{\sqrt{2}-\sqrt{3}}$+4×$\frac{1}{2\sqrt{2}}$-$\sqrt{（\sqrt{3}-2）^{2}}$
（2）$\sqrt{（-2）^{2}}$+|1-$\sqrt{2}$|+$\sqrt{3}$-$\frac{1}{\sqrt{3}-\sqrt{2}}$
（3）$\sqrt{12}$+$\frac{1}{2-\sqrt{3}}$-（2+$\sqrt{3}$）2
（4）（8-2$\sqrt{15}$）（$\sqrt{5}$+$\sqrt{3}$）2．
18．已知a，b互为相反数，c，d互为倒数，x的倒数等于-$\frac{1}{2}$，试求x2-（a+b+cd）x+（a+b）2015+（-cd）2014的值．
15．在数-5，1，-3，-2中任取三个数相乘，最小的积是-30．
2．观察下列等式：$\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，
将以上三个等式两边分别相加得：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
（1）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$；
（1）计算：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$；
（2）参照上述解法计算：$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$．
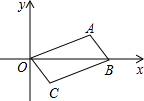12．如图，已知?OABC，其中O、A、B、C的坐标分别为O（0，0），A（3，a），B（4，0），C（b，-1）．
（1）求?OABC的对称中心的坐标．
（2）求a+b的值．
19．四个电子宠物排座位，一开始，小鼠，小猴，小兔，小猫分别坐在1，2，3，4号座位上（如图所示），以后它们不停地交换位置，第一次上下两排交换位置，第二次是在第一次交换位置后再左右两列交换位置，第三次再上下两排交换，第四次再左右两列交换位置，…，这样一直下去，第2008次交换位置后，小鼠所在的座号是（　　）
A．1B．2C．3D．4
16．在一个不透明的袋子中装有7个大小、形状完全相同的小球，小球上分别标有数字-2，-1，-$\frac{1}{2}$，0，$\frac{1}{2}$，1，2，摇匀后从中随机摸出一个小球，记小球上的数字为a，则a使得关于x的分式方程$\frac{a}{x+1}$-$\frac{2a-x-1}{{x}^{2}+x}$=0没有实数根的概率是$\frac{3}{7}$．
17．如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AC于E，EF⊥BC于F．求证：EF：DF=BC：AC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网