题目内容
16.在一个不透明的袋子中装有7个大小、形状完全相同的小球,小球上分别标有数字-2,-1,-$\frac{1}{2}$,0,$\frac{1}{2}$,1,2,摇匀后从中随机摸出一个小球,记小球上的数字为a,则a使得关于x的分式方程$\frac{a}{x+1}$-$\frac{2a-x-1}{{x}^{2}+x}$=0没有实数根的概率是$\frac{3}{7}$.分析 整理分式方程可得(a+1)x=2a-1,根据分式方程无解可分a=-1、a≠-1两种情况求得a的值,根据概率公式即可得答案.
解答 解:方程两边乘以x2+x得:ax-(2a-x-1)=0,
去括号,得:ax-2a+x+1=0,
移项,得:ax+x=2a-1,即(a+1)x=2a-1,
当a=-1时,方程无解;
当a≠-1时,解得:x=$\frac{2a-1}{a+1}$,
由此时方程无解可得$\frac{2a-1}{a+1}$=0或$\frac{2a-1}{a+1}$=-1,
解得:a=$\frac{1}{2}$或a=0,
综上,当a=-1、$\frac{1}{2}$、0时方程无解,
∴使得方程无实数根的概率为$\frac{3}{7}$,
故答案为:$\frac{3}{7}$.
点评 本题主要考查分式方程无解的情况和概率公式,根据分式方程无解得出a的值是解题的关键.

练习册系列答案
相关题目
11.中国人民银行授权中国外汇交易中心公布,2014年1月14日银行间外汇市场人民币汇率中间价为:1美元对人民币6.0930元,某上市公司持有美元资产为980万美元,用科学记数法表示其美元资产折合成人民币为( )元(保留两位有效数字)
| A. | 5.97×107 | B. | 6.0×107 | C. | 5.97×108 | D. | 6.0×108 |
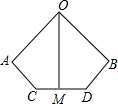 如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,M是CD中点.求证:OM是CD的垂直平分线.
如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,M是CD中点.求证:OM是CD的垂直平分线.