题目内容
12.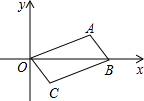 如图,已知?OABC,其中O、A、B、C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,-1).
如图,已知?OABC,其中O、A、B、C的坐标分别为O(0,0),A(3,a),B(4,0),C(b,-1).(1)求?OABC的对称中心的坐标.
(2)求a+b的值.
分析 (1)连接AC交BD于点D,根据平行四边形的性质和对称中心的概念得到点D是?OABC的对称中心,得到答案;
(2)作CE⊥OB于E,AF⊥OB于F,根据平行线的性质求出AF,得到a的值,求出OE,得到b的值,计算即可.
解答 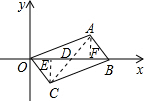 解:(1)连接AC交BD于点D,
解:(1)连接AC交BD于点D,
∵四边形OABC是平行四边形,
∴点D是?OABC的对称中心,
∵OB=4,
∴OD=$\frac{1}{2}$OB=2,
∴?OABC的对称中心的坐标为:(2,0);
(2)作CE⊥OB于E,AF⊥OB于F,
则CE∥AF,又AD=DC,
∴DE=DF,CE=AF=1,即a=1,
∵OB=4,OF=3,
∴BF=1,
∴OE=1,即b=1,
∴a+b=1+1=2.
点评 本题考查的是中心对称的概念和性质、平行四边形的性质以及坐标与图形的关系,掌握平行四边形的性质、中心对称的概念、正确作出辅助线是解题的关键.

练习册系列答案
相关题目
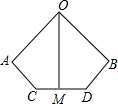 如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,M是CD中点.求证:OM是CD的垂直平分线.
如图,OA=OB,AC=BD,且OA⊥AC,OB⊥BD,M是CD中点.求证:OM是CD的垂直平分线.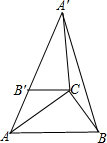 如图.在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕点C顺时针旋转得到的,其中点A′与点A是对应点,点B?与点B是对应点,已知A,B′,A′在同一条直线上.
如图.在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕点C顺时针旋转得到的,其中点A′与点A是对应点,点B?与点B是对应点,已知A,B′,A′在同一条直线上.