题目内容
17．
如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AC于E，EF⊥BC于F．求证：EF：DF=BC：AC．
分析 根据角平分线的性质，可得EF与AE的关系，根据平行线分线段成比例，可得AE：AC，根据比例的性质，可得AE：DF，根据相似三角形的判定与性质，可得AC：CD=BC：AC，根据等量代换，可得答案．
解答 证明：Rt△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AC于E，EF⊥BC于F，
∴EF=AE
∴EF：DF=AE：DF．
∵AD⊥BC，EF⊥BC，
∴AD∥EF，
∴AE：DF=AC：CD．
∵△ACD∽△BCA，
∴AC：CD=BC：AC
∴EF：DF=BC：AC．
点评 本题考查了相似三角形的判定与性质，利用平行线分线段成比例得出AE：DF=AC：CD是解题关键，又利用了相似三角形的判定与性质．
练习册系列答案
相关题目
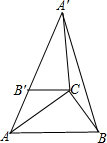如图．在Rt△ABC中，∠ABC=90°，∠B=60°，BC=2，△A′B′C是由△ABC绕点C顺时针旋转得到的，其中点A′与点A是对应点，点B?与点B是对应点，已知A，B′，A′在同一条直线上．