题目内容
9. 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):
(1)求y1的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)小丽应选择哪种销售方案,才能使月工资更多?
分析 (1)设l1所表示的函数关系式为y1=k1x,由待定系数法就可以求出解析式;
(2)由函数图象就可以得出方案二中每月付给销售人员的底薪是350元;
(3)由(1)可以求出方案1每件的提成,从而就可以求出方案2每件的提成,设销售m件时两种工资方案所得到的工资数额相等建立方程求出其解,可以得出销售方案即可.
解答 解:(1)设l1所表示的函数关系式为y1=k1x,由图象,得
420=30k1,
解得:k1=14,
∴l1所表示的函数关系式为y1=14x;
(2)∵每件商品的销售提成方案二比方案一少7元,
∴y2=(14-7)x+b 把(30,560)代入得560=7×30+b 解得b=350
∴方案二中每月付给销售人员的底薪是350元;
(3)由题意,得
方案1每件的提成为420÷30=14元,
∴方案2每件的提成为14-7=7元,
设销售m件时两种工资方案所得到的工资数额相等,由题意,得
14m=350+7m,
解得:m=50.
∴销售数量为50时,两种工资方案所得到的工资数额相等;
当销售件数少于50件时,提成方案2好些;
当销售件数等于50件时,两种提成方案一样;
当销售件数多于50件时,提成方案1好些.
点评 本题考查了待定系数法求一次函数的解析式的运用,一元一次方程的运用,设计方案的运用,解答时认真分析,弄清函数图象的意义是关键.

练习册系列答案
相关题目
1.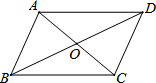 如图,下列四组条件中,能判定?ABCD是正方形的有( )
如图,下列四组条件中,能判定?ABCD是正方形的有( )
①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
 如图,下列四组条件中,能判定?ABCD是正方形的有( )
如图,下列四组条件中,能判定?ABCD是正方形的有( )①AB=BC,∠A=90°;②AC⊥BD,AC=BD;③OA=OD,BC=CD;④∠BOC=90°,∠ABD=∠DCA.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.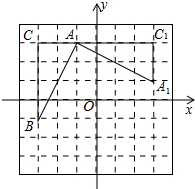 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.则旋转中心的坐标是( )| A. | (0,0) | B. | (-1,0) | C. | (1,0) | D. | (0,-1) |
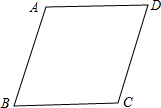 如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是16,则菱形ABCD的面积是$\frac{128\sqrt{3}}{9}$.
如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是16,则菱形ABCD的面积是$\frac{128\sqrt{3}}{9}$.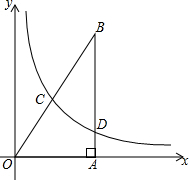 如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$.
如图,Rt△ABC中,∠OAB=90°,直角边OA在平面直角坐标系的x轴上,O为坐标原点,OA=2,AB=4,函数y=$\frac{k}{x}$(x>0)的图象分别与BO、BA交于C、D两点,且以B、C、D为顶点的三角形与△OAB相似,则k的值为$\frac{1}{2}$.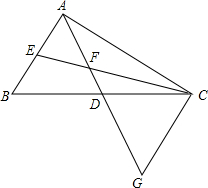 如图,△ABC中,D,E分别为BC,AB中点,连接EC,AD,且AD与EC交于点F,延长AD至点G使GD=AD,连结CG.
如图,△ABC中,D,E分别为BC,AB中点,连接EC,AD,且AD与EC交于点F,延长AD至点G使GD=AD,连结CG.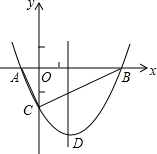 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).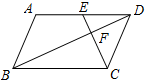 如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.