Question

20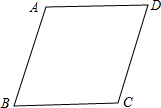．如图，在菱形ABCD中，∠BAD=120°．已知△ABC的周长是16，则菱形ABCD的面积是$\frac{128\sqrt{3}}{9}$．

Answer 1

分析 首先过点A作AE⊥BC于点E，连接AC，由在菱形ABCD中，∠BAD=120°，易证得△ABC是等边三角形，继而求得菱形的边长与高，则可求得答案．

解答 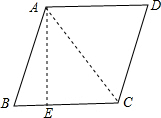解：过点A作AE⊥BC于点E，连接AC，
∵在菱形ABCD中，∠BAD=120°，
∴AB=BC，∠B=60°，
∴△ABC是等边三角形，
∵△ABC的周长是16，
∴AB=BC=$\frac{16}{3}$，
∴AE=AB•sin60°=$\frac{16}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{8}{3}$$\sqrt{3}$，
∴S_菱形ABCD=BC•AE=$\frac{16}{3}$×$\frac{8\sqrt{3}}{3}$=$\frac{128\sqrt{3}}{9}$．
故答案为：$\frac{128\sqrt{3}}{9}$．

点评 此题考查了菱形的性质以及等边三角形的判定与性质．注意证得△ABC是等边三角形是关键．