题目内容
19.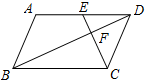 如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.(1)画出△DEC平移后的三角形;
(2)若BC=$2\sqrt{5}$,BD=6,CE=3,求AG的长.
分析 (1)由四边形ABCD是平行四边形,得出AD∥BC,AD=BC,将△DEC沿从D到A的方向平移,使点D与点A重合,则C与B重合,延长DA到G,使AG=DE,连结BG,则△AGB为所求;
(2)由平移的性质可得BG=CE=3,BG∥CE,而CE⊥BD,得出BG⊥BD.在Rt△BDG中利用勾股定理求出DG的长,进而得到AG的长.
解答 解:(1)△AGB为△DEC平移后的三角形,如下图所示;
(2)∵△AGB为△DEC平移后的三角形,
∴BG=CE=3,BG∥CE,
∵CE⊥BD,
∴BG⊥BD.
在Rt△BDG中,∵∠GBD=90°,BG=3,BD=6,
∴DG=$\sqrt{B{G}^{2}+B{D}^{2}}$=3$\sqrt{5}$,
∵四边形ABCD是平行四边形,
∴AD=BC=2$\sqrt{5}$,
∴AG=DG-AD=3$\sqrt{5}$-2$\sqrt{5}$=$\sqrt{5}$.
点评 本题考查了作图-平移变换,平移的性质,平行四边形的性质,作出点E平移后的点G是解题的关键.

练习册系列答案
相关题目
10.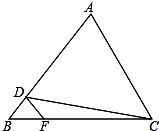 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
14.某校对该校八(1)班学生上学期期末考试数学成绩(成绩取整数,满分为100分,该班学生成绩均不低于50分)作了统计分析,绘制成如图频数分别直方图和频数、频率分别表,请你根据图表提供的信息,解答下列问题:
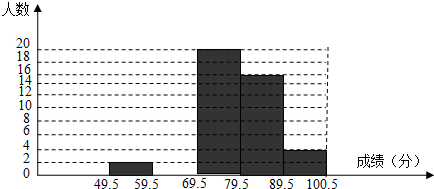
(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |

(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
8.下列运算正确的是( )
| A. | 6a-5a=1 | B. | (a2)3=a5 | C. | (-2x2y)3=-6x6y3 | D. | 3ab2•(-a)=-3a2b2 |
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题: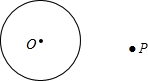 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)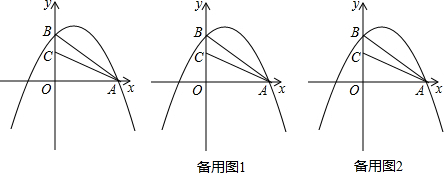
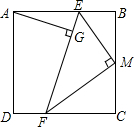 已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.
已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.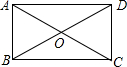 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.