题目内容
18.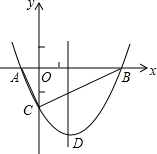 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
分析 (1)直接将(-1,0),代入解析式进而得出答案,再利用配方法求出函数顶点坐标;
(2)分别得出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,进而利用勾股定理的逆定理得出即可;
(3)利用轴对称最短路线求法得出M点位置,再求△ACM周长最小值.
解答 解:(1)∵点A(-1,0)在抛物线y=$\frac{1}{2}$x2+bx-2上,
∴$\frac{1}{2}$×(-1 )2+b×(-1)-2=0,
解得:b=-$\frac{3}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
y=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
∴顶点D的坐标为:($\frac{3}{2}$,-$\frac{25}{8}$);
(2)当x=0时y=-2,∴C(0,-2),OC=2.
当y=0时,$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,
解得:x1=-1,x2=4,
∴B (4,0),
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,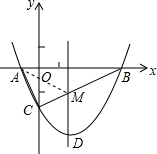
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
(3)如图所示:连接AM,
点A关于对称轴的对称点B,BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,
MC+MA的值最小,即△ACM周长最小,
设直线BC解析式为:y=kx+d,则$\left\{\begin{array}{l}{d=-2}\\{4k+d=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{d=-2}\\{k=\frac{1}{2}}\end{array}\right.$,
故直线BC的解析式为:y=$\frac{1}{2}$x-2,
当x=$\frac{3}{2}$时,y=-$\frac{5}{4}$,
∴M($\frac{3}{2}$,-$\frac{5}{4}$),
△ACM最小周长是:AC+AM+MC=AC+BC=$\sqrt{5}$+2$\sqrt{5}$=3$\sqrt{5}$.
点评 此题主要考查了二次函数综合以及利用轴对称求最短路线和勾股定理的逆定理等知识,得出M点位置是解题关键.

 阅读快车系列答案
阅读快车系列答案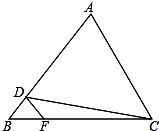 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
| A. | 6a-5a=1 | B. | (a2)3=a5 | C. | (-2x2y)3=-6x6y3 | D. | 3ab2•(-a)=-3a2b2 |
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题: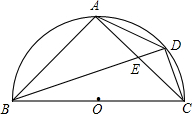 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.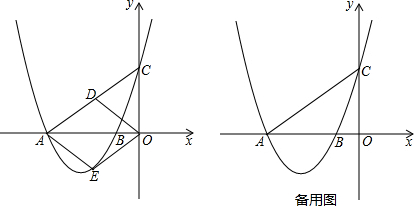
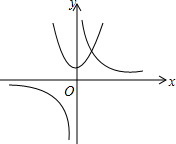 请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).
请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).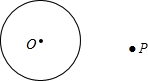 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)