题目内容
9.已知一次函数y=kx+b,当x=2时y的值是-1,当x=-1时y的值是5.(1)求此一次函数的解析式;
(2)若点P(m,n)是此函数图象上的一点,-3≤m≤2,求n的最大值.
分析 (1)把x=2,y=-1代入函数y=kx+b,得出方程组,求出方程组的解即可;
(2)把P点的坐标代入函数y=-2x+3,求出m的值,根据已知得出不等式组,求出不等式组的解集即可.
解答 解:(1)依题意得:$\left\{\begin{array}{l}{2k+b=-1}\\{-k+b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-2\\ b=3.\end{array}\right.$,
所以一次函数的解析式是y=-2x+3;
(2)由(1)可得,y=-2x+3.
∵点P (m,n ) 是此函数图象上的一点,
∴n=-2m+3即 $m=\frac{3-n}{2}$,
又∵-3≤m≤2,
∴$-3≤\frac{3-n}{2}≤2$,
解得,-1≤n≤9,
∴n的最大值是9.
点评 本题考查了用待定系数法求一次函数的解析式的应用,能求出函数的解析式是解此题的关键.

练习册系列答案
相关题目
1. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )
 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
18.下列判断中,正确的是( )
| A. | 有理数是有限小数 | B. | 无理数都是无限小数 | ||
| C. | 无限小数是无理数 | D. | 无理数没有算术平方根 |
 (1)求不等式组$\left\{\begin{array}{l}{x+3≥\frac{1}{2}x}\\{5-2x<9}\end{array}\right.$的解集;
(1)求不等式组$\left\{\begin{array}{l}{x+3≥\frac{1}{2}x}\\{5-2x<9}\end{array}\right.$的解集; 如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形.
如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形.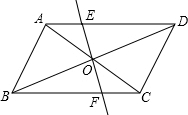 如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF.
如图,平行四边形ABCD的对角线相交于点O,过点O的任意一条直线与边AD相交于点E,与边BC相交于点F,求证:OE=OF. 已知;如图,在四边形ABCD中,点E、F在AC上,且AE=CF,若四边形EBFD是平行四边形.求证:四边形ABCD是平行四边形.
已知;如图,在四边形ABCD中,点E、F在AC上,且AE=CF,若四边形EBFD是平行四边形.求证:四边形ABCD是平行四边形. 如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4.
如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4.