题目内容
1. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠B=60°,则△ACD的面积为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 根据旋转的性质得AD=AB,得AD=CD,从而得△ACD的面积=△ABD的面积,出则根据等边三角形的判定方法可判断△ABD为等边三角形,然后根据等边三角形的面积公式求解.
解答 解:∵Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD为等边三角形,
∴AD=CD,
∴△ACD的面积=△ABD的面积=$\frac{\sqrt{3}}{4}$AB2=$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{4}$.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△ABD为等边三角形.

练习册系列答案
相关题目
12.下列四个条件中,不能判断四边形是平行四边形的条件是( )
| A. | 两组对边分别平行 | B. | 对角线互相平分 | ||
| C. | 两组对角分别相等 | D. | 一组对边平行,另一组对边相等 |
11. 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )
 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )| A. | AC=BD | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
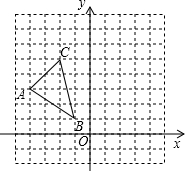 在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).
在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).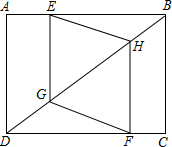 如图,矩形ABCD中,BC=3,AB=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE=$\frac{7}{8}$.
如图,矩形ABCD中,BC=3,AB=4,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE=$\frac{7}{8}$.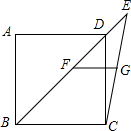 如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG,若AB=6,则FG的长度为3.
如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG,若AB=6,则FG的长度为3.