题目内容
19. 如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4.
如图所示,点C是线段AB上一点,AC<CB,M、N分别是AB、CB的中点,AC=8,NB=5,则线段MN=4.
分析 根据线段中点的性质,可得BC的长,根据线段的和差,可得AB的长,再根据线段中点的性质,可得BM的长,根据线段的和差,可得答案.
解答 解:由N是CB的中点,NB=5,得
BC=2NB=10.
由线段的和差,得
AB=AC+BC=8+10=18.
由M是AB的中点,得
MB=$\frac{1}{2}$AB=$\frac{1}{2}$×18=9.
由线段的和差,得
MN=MB-NB=9-5=4.
点评 本题考查了两点间的距离,利用线段中点的性质得出MB的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
 已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )
已知实数a在数轴上的位置如图所示,则化简|a-1|+$\sqrt{{a}^{2}}$的结果是( )| A. | -1 | B. | 1 | C. | 1-2a | D. | 2a-1 |
11. 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )
 如图,在?ABCD中,下列说法一定正确的是( )
如图,在?ABCD中,下列说法一定正确的是( )| A. | AC=BD | B. | AC⊥BD | C. | AB=CD | D. | AB=BC |
8.若a<b,则下列各式中不正确的是( )
| A. | a+3<b+3 | B. | a-3<b-3 | C. | -3a<-3b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
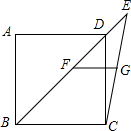 如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG,若AB=6,则FG的长度为3.
如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG,若AB=6,则FG的长度为3. 如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.
如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF. 已知$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是二元一次方程2x+y=a的一个解.
已知$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是二元一次方程2x+y=a的一个解.