题目内容
19．
（1）求不等式组$\left\{\begin{array}{l}{x+3≥\frac{1}{2}x}\\{5-2x＜9}\end{array}\right.$的解集；（2）如图，在△ABC中，己知∠ABC=30°，将△ABC绕点B逆时针旋转50°后得到△A′BC′，已知A′C′∥BC，求∠A的度数．
分析 （1）求出每个不等式的解集，再根据找不等式组解集的规律找出不等式组的解集即可；
（2）求出∠A′BC，根据平行线的性质求出∠A′，根据旋转的性质得出即可．
解答 解：（1）$\left\{\begin{array}{l}{x+3≥\frac{1}{2}x①}\\{5-2x＜9②}\end{array}\right.$，
∵解不等式①得：x≥-6，
解不等式②得：x＞-2，
∴不等式组的解集为x＞-2；
（2）∵将△ABC绕点B逆时针旋转50°后得到△A′BC′，
∠A′BA=50°，
∵∠ABC=30°，
∴∠A′BC=80°，
∵A′C′∥BC，
∴∠A′+∠A′BC=180°，
∴∠A′=100°，
∴根据旋转得出∠A=∠A′=100°．
点评 本题考查了解一元一次不等式组，旋转的性质，平行线的性质的应用，能根据不等式的解集找出不等式组的解集是解（1）小题的关键，能求出∠A′的度数是解（2）的关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
四边形ABCD是菱形，AC=16，DB=12，DH⊥AB于点H，求DH的长．
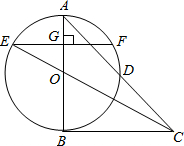如图，在△ABC中，∠A=45°，以AB为直径的⊙O交于AC的中点D，连接CO，CO的延长线交⊙O于点E，过点E作EF⊥AB，垂足为点G．
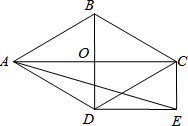如图，菱形ABCD的对角线AC和BD交于点O，分别过点C、D作CE∥BD，DE∥AC，CE和DE交于点E．
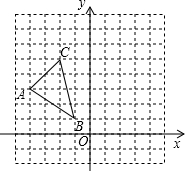在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系，并给出了格点△ABC（顶点是网格线的交点）．
