题目内容
17. 如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形.
如图,在直角坐标系中,四边形OABC的顶点O、A、C的坐标分别是(0,0)、(5,0)、(2,3),当点B的坐标为(7,3)时,四边形OABC是平行四边形.
分析 分别过点C、B作CE⊥x轴于点E,BD⊥x轴于点D,根据(2,3)可知OE=2,CE=3,再由HL定理得出△OCE≌△ABD,故可得出BD=CE=3,OE=AD=2,进可得出B点坐标.
解答  解:分别过点C、B作CE⊥x轴于点E,BD⊥x轴于点D,
解:分别过点C、B作CE⊥x轴于点E,BD⊥x轴于点D,
∵(2,3),
∴OE=2,CE=3.
∵四边形ABCD是平行四变形,
∴OC=AB,BC∥OA,
∴CE=BD,
在△OCE与△ABD中,
∵$\left\{\begin{array}{l}OC=AB\\ CE=BD\end{array}\right.$,
∴△OCE≌△ABD(HL),
∴BD=CE=3,OE=AD=2.
∵A(5,0),
∴OA=5,
∴OD=OA+AD=5+2=7,
∴B(7,3).
点评 本题考查的是平行四边形的判定,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
5.下列各式计算结果为-2的是( )
| A. | -(-2) | B. | (-$\frac{1}{2}$)-1 | C. | -12 | D. | $\sqrt{4}$ |
12.下列四个条件中,不能判断四边形是平行四边形的条件是( )
| A. | 两组对边分别平行 | B. | 对角线互相平分 | ||
| C. | 两组对角分别相等 | D. | 一组对边平行,另一组对边相等 |





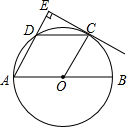 如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E 如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.
如图,在?ABCD中,点E、F在对角线BD的延长线上,且ED=FB,连结AE、EC、CF,AF.