题目内容
3.计算:(1)3$\sqrt{27}$+${(\sqrt{3}-1)}^{2}$-${(\frac{1}{2})}^{-1}$+$\frac{4}{\sqrt{3}+1}$
(2)$\left\{\begin{array}{l}2x+3y+z=6\\ x-y+2z=-1\\ x+2y-z=5\end{array}$
(3)$\sqrt{27}$÷[$\sqrt{48}$-(3$\sqrt{\frac{1}{3}}-2\sqrt{0.5}$)]
(4)$\left\{\begin{array}{l}2x+3y=15\\ \frac{x+1}{7}=\frac{y+4}{5}\end{array}$.
分析 (1)将各二次根式化为最简二次根式,然后合并同类项即可.
(2)利用消元法即可求出答案
(3)将各二次根式化为最简二次根式,然后根据乘法法则即可求出答案.
(4)先将分母去掉化简,然后利用消元法即可求出答案.
解答 解:(1)原式=9$\sqrt{3}$+4-2$\sqrt{3}$-2+2$\sqrt{3}$-2=9$\sqrt{3}$
(2)①+③得:3x+5y=11,④
①×2-②得:3x+7y=13,⑤
∴④-⑤得:y=1
将y=1代入④中,可得x=2,
将x=2,y=1代入①中,z=-1
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\\{z=-1}\end{array}\right.$
(3)原式=3$\sqrt{3}$÷(4$\sqrt{3}$-$\sqrt{3}$+$\sqrt{2}$)=$\frac{27-3\sqrt{6}}{25}$
(4)原方程组化为$\left\{\begin{array}{l}{2x+3y=15}\\{5x-7y=23}\end{array}\right.$
∴①×5得:10x+15y=75③
②×2得:10x-14y=46④
∴③-④得:y=1
将y=1代入2x+3y=15
∴x=6
∴方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$
点评 本题考查学生的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
14.$\sqrt{5}$介于下列哪两个整数之间( )
| A. | 0与1 | B. | 1与2 | C. | 2与3 | D. | 3与4 |
 如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.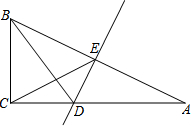 如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.